题目内容
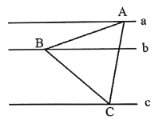
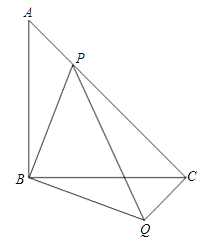
【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:PC=1:3时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
【答案】(1)90°;(2)2![]() ;(3)2PB2=PA2+PC2.
;(3)2PB2=PA2+PC2.
【解析】
(1)由于∠PCB=∠BCQ=45°,故有∠PCQ=90°.
(2)由等腰直角三角形的性质知,AC=4![]() ,根据已知条件,可求得AP,PC的值,再由勾股定理求得PQ的值.
,根据已知条件,可求得AP,PC的值,再由勾股定理求得PQ的值.
(3)由于△PBQ也是等腰直角三角形,故有PQ2=2PB2=PA2+PC2.
(1)由题意知,△ABP≌△CQB,
∴∠A=∠ACB=∠BCQ=45°,∠ABP=∠CPQ,AP=CQ,PB=BQ,
∴∠PCQ=∠ACB+∠BCQ=90°,∠ABP+∠PBC=∠CPQ+∠PBC=90°,
∴△BPQ是等腰直角三角形,△PCQ是直角三角形.
(2)当AB=4,AP:PC=1:3时,有AC=4![]() ,AP=
,AP=![]() ,PC=3
,PC=3![]() ,
,
∴PQ=![]() =2
=2![]() .
.
(3)存在2PB2=PA2+PC2,由于△BPQ是等腰直角三角形,
∴PQ=![]() PB.
PB.
∵AP=CQ,∴PQ2=PC2+CQ2=PA2+PC2,
故有2PB2=PA2+PC2.

练习册系列答案
相关题目