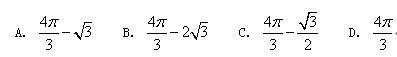题目内容
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
小题1:求证:直线PB与⊙O相切;
小题2:PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4,求CE的长.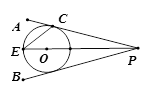
小题1:求证:直线PB与⊙O相切;
小题2:PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4,求CE的长.

小题1:见解析。
小题2:
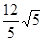
解:过O作OM垂直BP于M,连接OC。
∵⊙O与PA相切于点C.
∴ON垂直CP
∵点O在∠APB的平分线上,
∴OC=ON
∴直线PB与⊙O相切;
(2)由题意可得:OE=3,PC=4
连接OC,过C作CH垂直于PO
因为圆o与PA相切于点c,
所以∠OCP=90°
因为OE="OC=3,PC=4" , ∠OCP=90°
所以PO=5
有面积法可得CH=12/5
在Rt△OCH中,由勾股定理得到OH=9/5
所以EH=24/5
RT三角形CEH中,由勾股定理得到CE=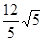
∵⊙O与PA相切于点C.
∴ON垂直CP
∵点O在∠APB的平分线上,
∴OC=ON
∴直线PB与⊙O相切;
(2)由题意可得:OE=3,PC=4
连接OC,过C作CH垂直于PO
因为圆o与PA相切于点c,
所以∠OCP=90°
因为OE="OC=3,PC=4" , ∠OCP=90°
所以PO=5
有面积法可得CH=12/5
在Rt△OCH中,由勾股定理得到OH=9/5
所以EH=24/5
RT三角形CEH中,由勾股定理得到CE=
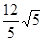

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
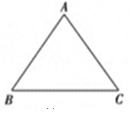
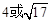 B.
B.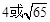
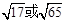 D.
D.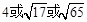
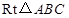 中,斜边
中,斜边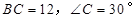 ,
,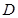 为
为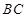 的中点,
的中点,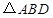 的外接圆
的外接圆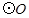 与
与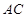 交于
交于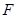 点,过
点,过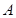 作
作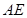 交
交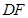 的延长线于
的延长线于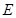 点.
点.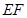 的长.
的长.
 ,⊙A和⊙B的位置关系是 。
,⊙A和⊙B的位置关系是 。
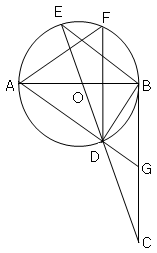
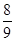 =0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 ▲ .
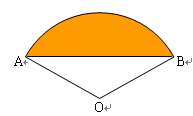
=0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 ▲ .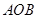 的圆心角为120°,半径为2,则图中阴影部分的面积为( )
的圆心角为120°,半径为2,则图中阴影部分的面积为( )