题目内容
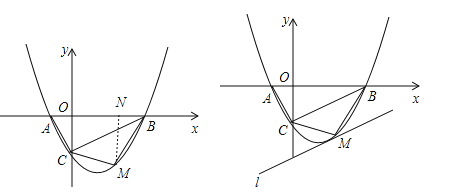
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)4,M(2,﹣3).
,0);(3)4,M(2,﹣3).
【解析】试题分析:方法一:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=![]() BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
方法二:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)通过求出A,B,C三点坐标,利用勾股定理或利用斜率垂直公式可求出AC⊥BC,从而求出圆心坐标.
(3)利用三角形面积公式,过M点作x轴垂线,水平底与铅垂高乘积的一半,得出△MBC的面积函数,从而求出M点.
试题解析:解:方法一:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,即:OC2=OAOB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(![]() ,0).
,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=![]() x﹣2;
x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=![]() x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b,当直线l与抛物线只有一个交点时,可列方程:
![]() x+b=
x+b=![]() ,即:
,即: ![]() ,且△=0;
,且△=0;
∴4﹣4×![]() (﹣2﹣b)=0,即b=﹣4;
(﹣2﹣b)=0,即b=﹣4;
∴直线l:y=![]() x﹣4.
x﹣4.
所以点M即直线l和抛物线的唯一交点,有:  ,解得:
,解得: ![]()
即 M(2,﹣3).
过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=![]() ×2×(2+3)+
×2×(2+3)+![]() ×2×3﹣
×2×3﹣![]() ×2×4=4.
×2×4=4.
方法二:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)∵y=![]() (x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=
(x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=![]() =﹣2,KBC=
=﹣2,KBC=![]() =
=![]() ,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(
,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(![]() ,0).
,0).
(3)过点M作x轴的垂线交BC′于H,∵B(4,0),C(0,﹣2),∴lBC:y=![]() x﹣2,设H(t,
x﹣2,设H(t, ![]() t﹣2),M(t,
t﹣2),M(t, ![]() ),∴S△MBC=
),∴S△MBC=![]() ×(HY﹣MY)(BX﹣CX)=
×(HY﹣MY)(BX﹣CX)=![]() ×(
×(![]() t﹣2﹣
t﹣2﹣![]() )(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).
)(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).

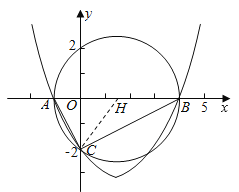

【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,已知该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
级别 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
频数(户) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)补全频率分布直方图;

(3)若将调查数据绘制成扇形统计图,则月均用水量“![]() ”的圆心角度数是 .
”的圆心角度数是 .