题目内容
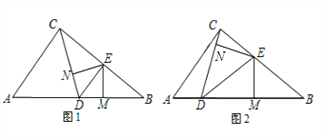
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,△BME与△CNE相似?
【答案】(1)见解析(2)AD=5或AD=4.8
【解析】试题分析:(1)当AD=CD时,要证明DE∥AC成立,只需要根据条件证明∠DAC=∠DCA=∠BDE=![]() ∠BDC即可;(2)分两种情况:①若△BME∽△CNE,②若△BME∽△ENC,分别讨论即可.
∠BDC即可;(2)分两种情况:①若△BME∽△CNE,②若△BME∽△ENC,分别讨论即可.
试题解析:(1)证明:∵AD="CD" ∴∠DAC=∠DCA
∴∠BDC=2∠DAC
又∵DE是∠BDC的平分线
∴∠DAC=∠BDE
∴DE∥AC
(2)解:分两种情况:
①若△BME∽△CNE,必有∠MBE=∠NCE
此时BD=DC
∵DE平分∠BDC
∴DE⊥BC,BE=EC
又∠ACB=90°
∴DE∥AC
∴![]() 即
即![]()
∴AD=5
②若△BME∽△ENC,必有∠EBM=∠CEN
此时NE∥MC
∵CD⊥NE,∴CD⊥AB
∴![]()
∴当AD=5或AD=4.8时,以B,M,E为顶点的三角形与以C,E,N为顶点的三角形相似……10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目