题目内容
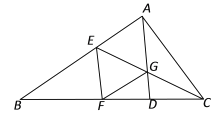
【题目】如图,点D、E分别是△ABC边BC、AB上的点,AD、CE相交于点G,过点E作EF∥AD交BC于点F,且![]() ,联结FG.
,联结FG.
(1)求证:GF∥AB;
(2)如果∠CAG=∠CFG,求证:四边形AEFG是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由![]() ,可得
,可得![]() ,再由EF∥AD,根据平行线分线段成比例定理可得
,再由EF∥AD,根据平行线分线段成比例定理可得 ![]() ,所以
,所以![]() ,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得
,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得 ![]() ,即
,即![]() ,再因
,再因![]() ,即可得
,即可得![]() ,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
试题解析:
(1)证明:∵![]() ,∴
,∴![]()
∵EF∥AD,∴ ![]()
∴![]()
∴GF∥AB
(2) 联结AF ,∵GF∥AB ∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∽
∽![]()
∴ ![]() ,即
,即![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∵GF∥AB,EF∥AD,∴四边形![]() 是平行四边形
是平行四边形
∴四边形![]() 是菱形
是菱形

练习册系列答案
相关题目