题目内容
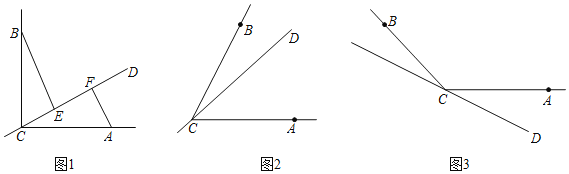
【题目】如图:![]() 、
、![]() 是锐角
是锐角![]() 的两条高,
的两条高,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,若EF=6,
的中点,若EF=6,![]() .
.
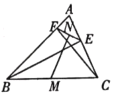
(1)证明:![]() ;
;
(2)判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求![]() 的长.
的长.
【答案】(1)证明见解析;(2)MN垂直平分EF,证明见解析;(3)MN=![]() .
.
【解析】
(1)依据BE、CF是锐角△ABC的两条高,可得∠ABE+∠A=90°,∠ACF+∠A=90°,进而得出∠ABE=∠ACF;
(2)连接EM、FM,根据直角三角形斜边上的中线等于斜边的一半可得EM=FM=![]() BC,再根据等腰三角形三线合一的性质解答;
BC,再根据等腰三角形三线合一的性质解答;
(3)求出EM、EN,然后利用勾股定理列式计算即可得解.
解:(1)∵BE、CF是锐角△ABC的两条高,
∴∠ABE+∠A=90°,∠ACF+∠A=90°,
∴∠ABE=∠ACF;
(2)MN垂直平分EF.
证明:如图,连接EM、FM,
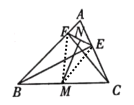
∵BE、CF是锐角△ABC的两条高,M是BC的中点,
∴EM=FM=![]() BC,
BC,
∵N是EF的中点,
∴MN垂直平分EF;
(3)∵EF=6,BC=24,
∴EM=![]() BC=
BC=![]() ×24=12,EN=
×24=12,EN=![]() EF=
EF=![]() ×6=3,
×6=3,
由勾股定理得,MN=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶![]() 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请估计
,请估计![]() 两地之间的距离.
两地之间的距离.
【题目】惠民超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多40件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
多40件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
甲种商品 | 乙种商品 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)惠民超市购进甲、乙两种商品各多少件?
(2)惠民超市将第一次购进的甲、乙两种商品全部卖完后一共可获利润多少元?
(3)惠民超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品每件降价1元销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多570元,求第二次乙商品是按原价打几折销售?