��Ŀ����
����Ŀ����֪CA��CB��CD�Ǿ�����BCA����C��һ��ֱ�ߣ�E��F��ֱ��CD�ϵ����㣬�ҡ�BEC����CFA������
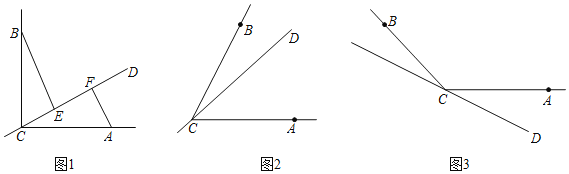
��1����ֱ��CD�ڡ�BCA���ڲ�����E��F������CD�ϣ����������������⣺
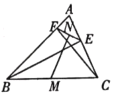
����ͼ1������BCA��90�㣬����90�㣬��BE�� ��CF��EF�� ��|BE��AF|�����������������������
����ͼ2����0�㣼��BCA��180�㣬������һ�����������BCA������ϵ�������� ����ʹ���е�����������Ȼ��������ȫͼ�β�֤����
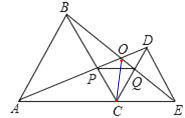
��2����ͼ3����ֱ��CD�ڡ�BCA���ⲿ����BCA���������õ�ʽֱ��д��EF��BE��AF�����߶ε�������ϵ�� ��������Ҫ��֤����
���𰸡���1����=��=���ڦ�+��BCA��180�㣬��ȫͼ�κ�֤������������2��EF��BE+AF
��������
��1���������BEC����AFC��90������CBE����ACF������AAS֤��BCE�ա�CAF���Ƴ�BE��CF��CE��AF���ɣ�
�������BEC����AFC����CBE����ACF������AAS֤��BCE�ա�CAF���Ƴ�BE��CF��CE��AF���ɣ�
��2�������BEC����AFC����CBE����ACF������AAS֤��BCE�ա�CAF���Ƴ�BE��CF��CE��AF���ɣ�
�⣺��1���١ߡ�BCA��90�����Ϧ���90����
���BCE+��CBE��90������BCE+��ACF��90����
���CBE����ACF��
��CA��CB����BEC����CFA��
���BCE�ա�CAF��ASA����
��BE��CF��EF��|CF��CE|��||BE��AF��
�ʴ�Ϊ����������
�ڦ�+��BCA��180������ȫͼ�����£�
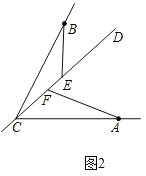
����BCE����CBE+��BCE��180������BEC��180��������
�ߡ�BCA��180��������
���BCA����CBE+��BCE��
���ߡ�ACF+��BCE����BCA��
���CBE����ACF��
����BC��CA����BEC����CFA��
���BCE�ա�CAF��AAS����
��BE��CF��CE��AF��
����EF��CE��CF��
��EF��|BE��AF|��
�ʴ�Ϊ����+��BCA��180����
��2��EF��BE+AF��
��ͼ3��
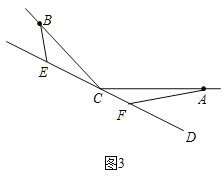
�ߡ�BEC����CFA������������BCA����BCA+��BCE+��ACF��180������CFA+��CAF+��ACF��180����
���BCE����CAF��
����BC��CA��
���BCE�ա�CAF��AAS����
��BE��CF��EC��FA��
��EF��EC+CF��BE+AF��
�ʴ�Ϊ��EF��BE+AF��