题目内容
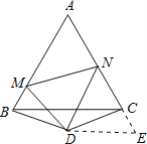
【题目】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.

【答案】BM+CN=NM,证明见解析
【解析】试题分析:延长AC至E,使CE=BM,连接DE,将BM,CN放在一条直线上,利用已知证明△DCE≌△BMD,再证出△DMN≌△DEN,从而得出答案.
试题解析:探究结论:BM+CN=NM.
证明:延长AC至E,使CE=BM,连接DE,
∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,
∴∠BCD=30°,
∴∠ABD=∠ACD=90°,
即∠ABD=∠DCE=90°,
∴在Rt△DCE和Rt△DBM中,
∵BD=CD,BM=EC
∴Rt△DCE≌Rt△DBM(HL),
∴∠BDM=∠CDE,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC﹣∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∴∠MDN=∠NDE=60°
∴DM=DE(上面已经全等)
在△DMN和△DEN中
∵DM=DE,∠MDN=∠NDE,DN=DN
∴△DMN≌△DEN(SAS),
∴NM=EN
即NM=CE+CN
∴BM+CN=NM.

练习册系列答案
相关题目






