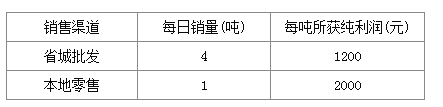
ЬтФПФкШн
ЁОЬтФПЁП(1)ЬюПе21Ѓ20ЃН2( )ЃЛ 22Ѓ21ЃН2( ) ЃЛ23 Ѓ22ЃН2( )
(2)ЧыгУзжФИБэЪОЕкnИіЕШЪНЃЌВЂбщжЄФуЕФЗЂЯжЃЎ
(3)РћгУ(2)жаФуЕФЗЂЯжЃЌЧѓ20ЃЋ21ЃЋ22ЃЋ23ЃЋЁЃЋ22016ЃЋ22017ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0ЃЌ1ЃЌ2ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОн0ДЮУнЕФвтвхКЭГЫЗНЕФвтвхНјааМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЙлВьИїЕШЪНЕУЕН2ЕФЯрСкСНИіЗЧИКећЪ§УнЕФВюЕШгкЦфжаНЯаЁЕФ2ЕФЗЧИКећЪ§УнЃЌМД2n-2n-1=2n-1ЃЈnЮЊе§ећЪ§ЃЉЃЛ
ЃЈ3ЃЉгЩгк21-20=20ЃЌ22-21=21ЃЌ23-22=22ЃЌЁ22018-22017=22017ЃЌШЛКѓАбЕШЪНзѓБпгызѓБпЯрМгЃЌгвБпгыгвБпЯрМгМДПЩЧѓНтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ21-20=1=20ЃЛ22-21=2=21ЃЛ23-22=4=22ЃЌ
ЙЪД№АИЮЊЃК0ЃЌ1ЃЌ2ЃЛ
ЃЈ2ЃЉЙлВьПЩЕУЃК2n-2n-1=2n-1ЃЈnЮЊе§ећЪ§ЃЉЃЌжЄУїШчЯТЃК
2n-2n-1=2ЁС2n-1-2n-1=2n-1ЁС(2-1)=2n-1ЃЛ
ЃЈ3ЃЉЁп21-20=20ЃЌ
22-21=21ЃЌ
23-22=22ЃЌ
Ё
22018-22017=22017ЃЌ
Ёр22018-20=20+21+22+23+Ё+22016+22017ЃЌ
Ёр20+21+22+23+Ё+22016+22017ЕФжЕЮЊ22018-1ЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
27
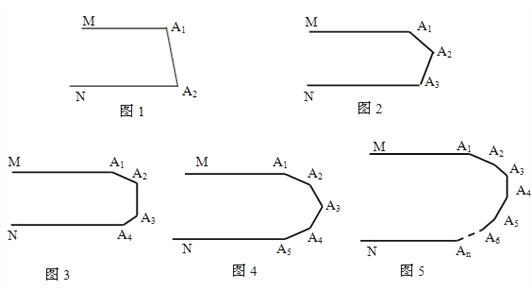
ЁОЬтФПЁП(1) ШчЭМ1ЃЌMA1ЁЮNA2ЃЌдђЁЯA1+ЁЯA2=_________ЖШЃЎ
ШчЭМ2ЃЌMA1ЁЮNA3ЃЌдђЁЯA1+ЁЯA2+ЁЯA3=_________ ЖШЃЎ
ШчЭМ3ЃЌMA1ЁЮNA4ЃЌдђЁЯA1+ЁЯA2+ЁЯA3+ЁЯA4=_________ЖШЃЎ
ШчЭМ4ЃЌMA1ЁЮNA5ЃЌдђЁЯA1+ЁЯA2+ЁЯA3+ЁЯA4+ЁЯA5=_________ЖШЃЎ
ШчЭМ5ЃЌMA1ЁЮNAnЃЌдђЁЯA1+ЁЯA2+ЁЯA3+Ё+ЁЯAn=_________ ЖШЃЎ
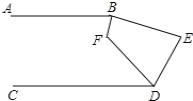
(2) ШчЭМ,вбжЊABЁЮCD,ЁЯABEКЭЁЯCDEЕФЦНЗжЯпЯрНЛгкF,ЁЯE=80ЁуЃЌЧѓЁЯBFDЕФЖШЪ§.
ЁОД№АИЁПЃЈ1ЃЉ 180ЃЛ 360ЃЛ 540ЃЛ720ЃЛ180ЃЈn-1ЃЉЃЛЃЈ2ЃЉ140Ёу.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШЙ§ИїЕузїMA 1 ЕФЦНааЯпЃЌгЩMA 1 ЁЮNA 2 ЃЌПЩЕУИїЯпЦНааЃЌИљОнСНжБЯпЦНааЃЌЭЌХдФкНЧЛЅВЙЃЌМДПЩЧѓЕУД№АИЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжаЕФЙцТЩПЩЕУЁЯABE+ЁЯE+ЁЯCDE=360ЁуЃЌЫљвдЁЯABE+ЁЯCDE=360Ёу-80Ёу=280ЁуЃЌгжвђЮЊBFЁЂDFЦНЗжЁЯABEКЭЁЯCDEЃЌЫљвдЁЯFBE+ЁЯFDE=140ЁуЃЌгжвђЮЊЫФБпаЮЕФФкНЧКЭЮЊ360ЁуЃЌНјЖјПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌ
ЁпMA 1 ЁЮNA 2 ЃЌ
ЁрЁЯA 1 +ЁЯA 2 =180ЁуЃЎ
ШчЭМ2ЃЌЙ§ЕуA 2 зїA 2 C 1 ЁЮA 1 MЃЌ
ЁпMA 1 ЁЮNA 3 ЃЌ
ЁрA 2 C 1 ЁЮA 1 MЁЮNA 3 ЃЌ
ЁрЁЯA 1 +ЁЯA 1 A 2 C 1 =180ЁуЃЌЁЯC 1 A 2 A 3 +ЁЯA 3 =180ЁуЃЌ
ЁрЁЯA 1 +ЁЯA 2 +ЁЯA 3 =360ЁуЃЎ
ШчЭМ3ЃЌЙ§ЕуA 2 зїA 2 C 1 ЁЮA 1 MЃЌЙ§ЕуA 3 зїA 3 C 2 ЁЮA 1 MЃЌ
ЁпMA 1 ЁЮNA 3 ЃЌ
ЁрA 2 C 1 ЁЮA 3 C 2 ЁЮA 1 MЁЮNA 3 ЃЌ
ЁрЁЯA 1 +ЁЯA 1 A 2 C 1 =180ЁуЃЌЁЯC 1 A 2 A 3 +ЁЯA 2 A 3 C 2 =180ЁуЃЌЁЯC 2 A 3 A 4 +ЁЯA 4 =180ЁуЃЌ
ЁрЁЯA 1 +ЁЯA 2 +ЁЯA 3 +ЁЯA 4 =540ЁуЃЎ
ШчЭМ4ЃЌЙ§ЕуA 2 зїA 2 C 1 ЁЮA 1 MЃЌЙ§ЕуA 3 зїA 3 C 2 ЁЮA 1 MЃЌ
ЁпMA 1 ЁЮNA 3 ЃЌ
ЁрA 2 C 1 ЁЮA 3 C 2 ЁЮA 1 MЁЮNA 3 ЃЌ
ЁрЁЯA 1 +ЁЯA 1 A 2 C 1 =180ЁуЃЌЁЯC 1 A 2 A 3 +ЁЯA 2 A 3 C 2 =180ЁуЃЌЁЯC 2 A 3 A 4 +ЁЯA 3 A 4 C 3 =180ЁуЃЌЁЯC 3 A 4 A 5 +ЁЯA 5 =180ЁуЃЌ
ЁрЁЯA 1 +ЁЯA 2 +ЁЯA 3 +ЁЯA 4 +ЁЯA 5 =720ЁуЃЛ
ДгЩЯЪіНсТлжаФуЗЂЯжСЫЙцТЩЃКШчЭМ5ЃЌMA 1 ЁЮNA n ЃЌдђЁЯA 1 +ЁЯA 2 +ЁЯA 3 +Ё+ЁЯA n =180ЃЈn-1ЃЉЖШЃЌ
ЙЪД№АИЮЊЃК180ЃЌ360ЃЌ540ЃЌ720ЃЌ180ЃЈn-1ЃЉЃЛ

ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУЁЯABE+ЁЯE+ЁЯCDE=360ЁуЃЌ
ЁпЁЯE=80ЁуЃЌ
ЁрЁЯABE+ЁЯCDE=360Ёу-80Ёу=280ЁуЃЌ
гжЁпBFЁЂDFЦНЗжЁЯABEКЭЁЯCDEЃЌ
ЁрЁЯFBE+ЁЯFDE=140ЁуЃЌ
ЁпЁЯFBE+ЁЯE+ЁЯFDE+ЁЯBFD=360ЁуЃЌ
ЁрЁЯBFD=360Ёу-80Ёу-140Ёу=140ЁуЃЎ

 ЦкФЉКУГЩМЈЯЕСаД№АИ
ЦкФЉКУГЩМЈЯЕСаД№АИ 99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ
99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ
АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ