题目内容
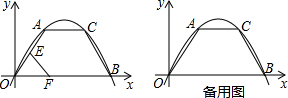
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且tan∠ACO=
,CO=BO,AB=3,求这条抛物线的函数解析式.

| 1 |
| 2 |

据题意设CO=BO=t(t>0)(1分)
在Rt△OCA中,tan∠ACO=
=
∴AO=
CO=
t
∵AB=3
∴AO+BO=
t+t=3,解得t=2(2分)
∴A(-1,0),B(2,0),C(0,-2)(3分)
代入y=ax2+bx+c得
,
解得
(3分)
∴所求函数解析式为y=x2-x-2(1分)
在Rt△OCA中,tan∠ACO=
| AO |
| CO |
| 1 |
| 2 |
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=3
∴AO+BO=
| 1 |
| 2 |
∴A(-1,0),B(2,0),C(0,-2)(3分)
代入y=ax2+bx+c得
|
解得
|
∴所求函数解析式为y=x2-x-2(1分)

练习册系列答案
相关题目
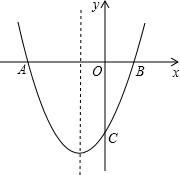
 为A(-1,0),C(0,-3).
为A(-1,0),C(0,-3).