题目内容
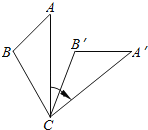
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
A.110° B.80° C.40° D.30°
【答案】B
【解析】
试题分析:首先根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,即可得到∠A′=40°,再有∠B′=110°,利用三角形内角和可得∠A′CB′的度数,进而得到∠ACB的度数,再由条件将△ABC绕着点C顺时针旋转50°后得到△A′B′C′可得∠ACA′=50°,即可得到∠BCA′的度数.
解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°﹣110°﹣40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°,
故选:B.

练习册系列答案
相关题目