题目内容
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
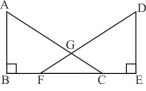
求证:(1)△ABC≌△DEF;
(2)GF=GC。
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据全等三角形的判定定理SAS证得△ABC≌△DEF;
(2)由(1)中的全等三角形的对应角相等推知∠ACB=∠DFE,然后由“等角对等边”证得结论.
试题解析:(1)∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
又∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在△ABC和△DEF中,
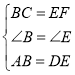 ,
,
∴△ABC≌△DEF (SAS)
(2)∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴GF=GC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目