题目内容
【题目】如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE。
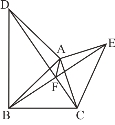
(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由。
【答案】(1)证明见解析;(2)∠AFD=∠AFE.理由见解析.
【解析】
试题分析:(1)求出∠DAC=∠BAE,根据SAS得出△DAC≌△BAE,即可得出结论;
(2)根据全等三角形的性质得出两三角形面积相等和DC=BE,根据面积公式求出AM=AN,根据角平分线的判定方法即可得出结论.
试题解析:(1)∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又AD=AB,AC=AE,
∴△DAC≌△BAE(SAS),
∴DC=BE.
(2)∠AFD=∠AFE,理由如下:
过A作AM⊥DC于M,AN⊥BE于N,如图所示:
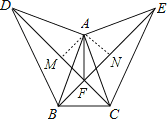
∵△DAC≌△BAE,
∴S△ACD=S△ABE,DC=BE,
∴![]() DC×AM=
DC×AM=![]() BE×AN,
BE×AN,
∴AM=AN,
∴点A在∠DFE的平分线上,
∴∠AFD=∠AFE.

练习册系列答案
相关题目