题目内容
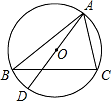如图，AD是△ABC的外接圆直径，AD=
，∠B=∠DAC，则AC的值为________．
1
分析：连接CD，由圆周角定理可知∠ACD=90°，再根据∠DAC=∠ABC可知AC=CD，由勾股定理即可得出AC的长．
解答：
解：连接CD，
∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠DAC=∠ABC，∠ABC=∠ADC，
∴∠DAC=∠ADC，
∴
=
，
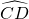∴AC=CD，
又∵AC2+CD2=AD2，
∴2AC2=AD2，
∵AD=，
∴AC=
=1．
故答案为：1．
点评：本题考查的是圆周角定理及勾股定理、直角三角形的性质，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
分析：连接CD，由圆周角定理可知∠ACD=90°，再根据∠DAC=∠ABC可知AC=CD，由勾股定理即可得出AC的长．
解答：
解：连接CD，∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠DAC=∠ABC，∠ABC=∠ADC，
∴∠DAC=∠ADC，
∴
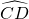=，∴AC=CD，
又∵AC2+CD2=AD2，
∴2AC2=AD2，
∵AD=
，∴AC=
=1．故答案为：1．
点评：本题考查的是圆周角定理及勾股定理、直角三角形的性质，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
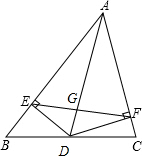如图，AD是△ABC是角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G，则AD与EF的位置关系是
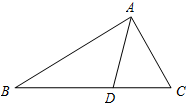16、已知：如图，AD是△ABC的角平分线，且 AB：AC=3：2，则△ABD与△ACD的面积之比为
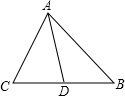如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm．
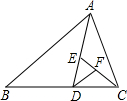如图，AD是△ABC的中线，CE是△ACD的中线，DF是△CDE的中线，如果△DEF的面积是2，那么△ABC的面积为（ ）