题目内容
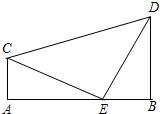 如图,AC⊥AB,DB⊥AB,垂足分别为A、B,点E在线段AB上,且BE=AC,CE=DE.
如图,AC⊥AB,DB⊥AB,垂足分别为A、B,点E在线段AB上,且BE=AC,CE=DE.
(1)求证:△CAE≌△EBD;
(2)已知AC=4,CD=10,求CE和BD的长.
(1)证明:∵AC⊥AB,DB⊥AB,
∴∠A=∠B=90°.
在Rt△CAE和Rt△EBD中
BE=AC,CE=DE,
∴△CAE≌△EBD.
(2)解:在Rt△CED中
∵CE=DE,CD=10,
∴CE=DE=5 .
.
在Rt△CAE中
∵AC=4,CE=5 ,
,
∴AE= .
.
∵△CAE≌△EBD,
∴BD=AE= .
.
分析:(1)因为AC⊥AB,DB⊥AB,所以∠A=∠B=90°,在Rt△CAE和Rt△EBD中,BE=AC,CE=DE,故可根据HL判定两三角形全等;
(2)在Rt△CED中,因为CE=DE,CD=10,所以CE=DE=5 ,在Rt△CAE中,因为AC=4,CE=5
,在Rt△CAE中,因为AC=4,CE=5 ,所以AE=
,所以AE= ,又因为△CAE≌△EBD,所以BD=AE=
,又因为△CAE≌△EBD,所以BD=AE= .
.
点评:本题考查了三角形全等的判定及性质;此题把全等三角形的判定和全等三角形的性质综合求解.有利于培养学生综合运用数学知识的能力.
∴∠A=∠B=90°.
在Rt△CAE和Rt△EBD中
BE=AC,CE=DE,
∴△CAE≌△EBD.
(2)解:在Rt△CED中
∵CE=DE,CD=10,
∴CE=DE=5
 .
.在Rt△CAE中
∵AC=4,CE=5
 ,
,∴AE=
 .
.∵△CAE≌△EBD,
∴BD=AE=
 .
.分析:(1)因为AC⊥AB,DB⊥AB,所以∠A=∠B=90°,在Rt△CAE和Rt△EBD中,BE=AC,CE=DE,故可根据HL判定两三角形全等;
(2)在Rt△CED中,因为CE=DE,CD=10,所以CE=DE=5
 ,在Rt△CAE中,因为AC=4,CE=5
,在Rt△CAE中,因为AC=4,CE=5 ,所以AE=
,所以AE= ,又因为△CAE≌△EBD,所以BD=AE=
,又因为△CAE≌△EBD,所以BD=AE= .
.点评:本题考查了三角形全等的判定及性质;此题把全等三角形的判定和全等三角形的性质综合求解.有利于培养学生综合运用数学知识的能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
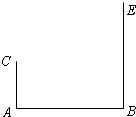 21、如图,AC⊥AB,BE⊥AB,AB=10,AC=2.用一块三角尺进行如下操作:将直角顶点P在线段AB上滑动,一直角边始终经过点C,另一直角边与BE相交于点D,若BD=8,则AP的长为
21、如图,AC⊥AB,BE⊥AB,AB=10,AC=2.用一块三角尺进行如下操作:将直角顶点P在线段AB上滑动,一直角边始终经过点C,另一直角边与BE相交于点D,若BD=8,则AP的长为
 4、如图,AC=AB,AD平分∠CAB,E在AD上,则图中能全等的三角形有( )对.
4、如图,AC=AB,AD平分∠CAB,E在AD上,则图中能全等的三角形有( )对.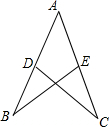 如图,AC=AB,BD=CE,若∠B=25°,则∠C=
如图,AC=AB,BD=CE,若∠B=25°,则∠C= 如图,AC⊥AB,AD⊥AE,且AB=AC,AD=AE,探究BD与CE的关系.
如图,AC⊥AB,AD⊥AE,且AB=AC,AD=AE,探究BD与CE的关系.