Question

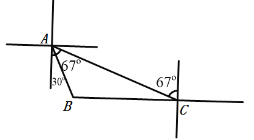
【题目】如图，观测站C发现在它的正西方向，有一艘渔船B出现险情，需救援，当即上报救援中心A，测得C在A的南偏东67方向，距A处50海里，而B在A的南偏东30方向，求渔船B与救援中心A的距离AB，渔船B与观测站C的距离BC．（结果精确到0.1海里）（参考数据：sin37=0.6，cos37=0.8，tan37=，≈1.73）

Answer 1

【答案】AB的长约为23.7海里，BC的长约为34.6海里

【解析】

过点C，作CD⊥AB，交AB的延长线于点D，构造Rt△ABC，求出AD、CD，根据三角函数值求出BC即可．

解：过点C，作CD⊥AB，交AB的延长线于点D，构造Rt△ABC，求出AD、CD，根据三角函数值求出BC即可．

在Rt△ABC中，

cos37=，

∴AD=50×0.8=40，

CD=50×sin37=30 ，

∴在Rt△BCD中，

∵B在A的南偏东30方向，

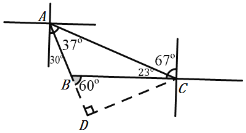
∴∠DBC= 60 ，

∴tan60=，

∴BD=10，

∴AB=40-，

≈40-10×1.73

=23.7．

又∵cos60=，

∴BC=20≈34.6，

答：AB的长约为23.7海里，BC的长约为34.6海里．