题目内容
下列命题:①若x2=2010×2012+1,则x=2011;②若xy<0,且| a-2y+1 |
| 2 |
| 1 |
| 2 |
其中正确的命题的序号为
分析:①把2010看作2011-1,2012看作2011+1,然后利用平方差公式化简合并后,开方即可求出x的值,即可得到本命题的真假;
②根据两非负数的和为0,得到两非负数同时为0,即可求出a与y的关系式及x的值,根据xy<0,即可求出a的取值范围,即可判断本命题的真假;
③设出此梯形的上底与下底,然后根据勾股定理列出方程,根据上下底都为整数,即可得到上下底的值,进而求出梯形的高,即可判断本命题的真假;
④根据方程的一个解为1,代入方程得到a+b+c=0,又a>b>c,得到a一定大于0,而方程的另外一个根为k,则方程化为a(x-1)(x-k)=0,化简后分别用a表示出b和c,利用a>b>c列出关于k与a的不等式,当a大于0,即可得到k的取值范围.
②根据两非负数的和为0,得到两非负数同时为0,即可求出a与y的关系式及x的值,根据xy<0,即可求出a的取值范围,即可判断本命题的真假;
③设出此梯形的上底与下底,然后根据勾股定理列出方程,根据上下底都为整数,即可得到上下底的值,进而求出梯形的高,即可判断本命题的真假;
④根据方程的一个解为1,代入方程得到a+b+c=0,又a>b>c,得到a一定大于0,而方程的另外一个根为k,则方程化为a(x-1)(x-k)=0,化简后分别用a表示出b和c,利用a>b>c列出关于k与a的不等式,当a大于0,即可得到k的取值范围.
解答:解:①x2=2010×2012+1=(2011-1)(2011+1)+1=20112-1+1=20112,
开方得:x=±2011,本命题为假命题;
②由
+(x+1)2=0,得到a-2y+1=0且x+1=0,
解得:x=-1<0,y=
,又xy<0,
所以得到
>0,
解得a>-1,本命题为真命题;
③设此直角梯形的上下底分别为x与y,高为z,
根据勾股定理得:112-x2=92-y2=z2,
所以x2-y2=40,即(x+y)(x-y)=40,
因为x与y为整数,所以当x+y=20,x-y=2时,联立解得x=11,y=9,代入得z=0,舍去;
当x+y=10,x-y=4时,联立解得x=7,y=3.
所以此直角梯形的上底为3,下底为7,高Z=
=
=6
,本命题正确;
④因为方程的一根为1,另一根为k,
把x=1代入方程得:a+b+c=0,又因为a>b>c,
所以a>0,
则方程可化为a(x-1)(x-k)=0,
化简得:ax2-a(k+1)x+ak=0,又方程ax2+bx+c=0,
得到b=-ak-a,c=ak,又a>b>c,
所以有-ak-a>ak,且由a>-ak-a,
当a>0时,解得:-2<k<-
;
所以,方程另一根的取值范围是:-2<k<-
,本命题正确.
故正确答案为序号有:②③④.
故答案为:②③④
开方得:x=±2011,本命题为假命题;
②由
| a-2y+1 |
解得:x=-1<0,y=
| a+1 |
| 2 |
所以得到
| a+1 |
| 2 |
解得a>-1,本命题为真命题;
③设此直角梯形的上下底分别为x与y,高为z,
根据勾股定理得:112-x2=92-y2=z2,
所以x2-y2=40,即(x+y)(x-y)=40,
因为x与y为整数,所以当x+y=20,x-y=2时,联立解得x=11,y=9,代入得z=0,舍去;
当x+y=10,x-y=4时,联立解得x=7,y=3.
所以此直角梯形的上底为3,下底为7,高Z=
| 92-32 |
| 72 |
| 2 |
④因为方程的一根为1,另一根为k,
把x=1代入方程得:a+b+c=0,又因为a>b>c,
所以a>0,
则方程可化为a(x-1)(x-k)=0,
化简得:ax2-a(k+1)x+ak=0,又方程ax2+bx+c=0,
得到b=-ak-a,c=ak,又a>b>c,
所以有-ak-a>ak,且由a>-ak-a,
当a>0时,解得:-2<k<-
| 1 |
| 2 |
所以,方程另一根的取值范围是:-2<k<-
| 1 |
| 2 |
故正确答案为序号有:②③④.
故答案为:②③④
点评:此题考查学生灵活运用平方差公式化简求值,掌握两非负数之和为0时的条件,是一道综合题.

练习册系列答案
相关题目
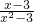 =0的解;③有公共顶点且相等的角是对顶角;④在两个三角形中,两边对应相等,且其中一组相等的边所对的角相等,则这两个三角形全等;⑤如果|a|=|b|,则a=b;⑥在三角形中若一边上的中线等于这一边的一半,则这个三角形是直角三角形且这一边所对的角是直角;是真命题的有几个
=0的解;③有公共顶点且相等的角是对顶角;④在两个三角形中,两边对应相等,且其中一组相等的边所对的角相等,则这两个三角形全等;⑤如果|a|=|b|,则a=b;⑥在三角形中若一边上的中线等于这一边的一半,则这个三角形是直角三角形且这一边所对的角是直角;是真命题的有几个