题目内容
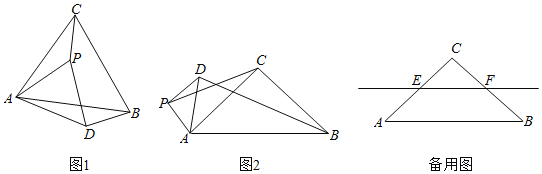
【题目】问题提出:如图1,在等边△ABC中,AB=12,⊙C半径为6,P为圆上一动点,连结AP,BP,求AP+![]() BP的最小值.
BP的最小值.

(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=3,则有![]() =
=![]() =
=![]() ,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴![]() =
=![]() ,∴PD=
,∴PD=![]() BP,∴AP+
BP,∴AP+![]() BP=AP+PD.请你完成余下的思考,并直接写出答案:AP+
BP=AP+PD.请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为.
BP的最小值为.
(2)自主探索:如图1,矩形ABCD中,BC=7,AB=9,P为矩形内部一点,且PB=3,![]() AP+PC的最小值为.
AP+PC的最小值为.
(3)拓展延伸:如图2,扇形COD中,O为圆心,∠COD=120°,OC=4,OA=2,OB=3,点P是![]() 上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
上一点,求2PA+PB的最小值,画出示意图并写出求解过程.

【答案】(1)AP+![]() BP的最小值为3
BP的最小值为3![]() ;(2)
;(2)![]() AP+PC的值最小值为5
AP+PC的值最小值为5![]() ;(3)2PA+PB的最小值为
;(3)2PA+PB的最小值为![]() ,见解析.
,见解析.
【解析】
(1)由等边三角形的性质可得CF=6,AF=6![]() ,由勾股定理可求AD的长;
,由勾股定理可求AD的长;
(2)在AB上截取BF=1,连接PF,PC,由![]() ,可证△ABP∽△PBF,可得PF=
,可证△ABP∽△PBF,可得PF=![]() AP,即
AP,即![]() AP+PC=PF+PC,则当点F,点P,点C三点共线时,
AP+PC=PF+PC,则当点F,点P,点C三点共线时,![]() AP+PC的值最小,由勾股定理可求
AP+PC的值最小,由勾股定理可求![]() AP+PC的值最小值;
AP+PC的值最小值;
(3)延长OC,使CF=4,连接BF,OP,PF,过点F作FB⊥OD于点M,由![]() ,可得△AOP∽△POF,可得PF=2AP,即2PA+PB=PF+PB,则当点F,点P,点B三点共线时,2AP+PB的值最小,由勾股定理可求2PA+PB的最小值.
,可得△AOP∽△POF,可得PF=2AP,即2PA+PB=PF+PB,则当点F,点P,点B三点共线时,2AP+PB的值最小,由勾股定理可求2PA+PB的最小值.
解:(1)解:(1)如图1,

连结AD,过点A作AF⊥CB于点F,
∵AP+![]() BP=AP+PD,要使AP+
BP=AP+PD,要使AP+![]() BP最小,
BP最小,
∴AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,
即:AP+![]() BP最小值为AD,
BP最小值为AD,
∵AC=12,AF⊥BC,∠ACB=60°
∴CF=6,AF=6![]()
∴DF=CF-CD=6-3=3
∴AD=![]() =3
=3![]()
∴AP+![]() BP的最小值为3
BP的最小值为3![]()
(2)如图,
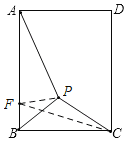
在AB上截取BF=1,连接PF,PC,
∵AB=9,PB=3,BF=1
∴![]() ,且∠ABP=∠ABP,
,且∠ABP=∠ABP,
∴△ABP∽△PBF,
∴![]()
∴PF=![]() AP
AP
∴![]() AP+PC=PF+PC,
AP+PC=PF+PC,
∴当点F,点P,点C三点共线时,![]() AP+PC的值最小,
AP+PC的值最小,
∴CF=![]() =
=![]() =5
=5![]()
∴![]() AP+PC的值最小值为5
AP+PC的值最小值为5![]() ,
,
(3)如图,
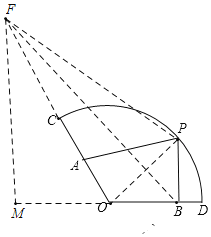
延长OC,使CF=4,连接BF,OP,PF,过点F作FB⊥OD于点M,
∵OC=4,FC=4,
∴FO=8,且OP=4,OA=2,
∴![]() ,且∠AOP=∠AOP
,且∠AOP=∠AOP
∴△AOP∽△POF
∴![]()
∴PF=2AP
∴2PA+PB=PF+PB,
∴当点F,点P,点B三点共线时,2AP+PB的值最小,
∵∠COD=120°,
∴∠FOM=60°,且FO=8,FM⊥OM
∴OM=4,FM=4![]()
∴MB=OM+OB=4+3=7
∴FB=![]() =
=![]()
∴2PA+PB的最小值为![]() .
.

【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:《满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲 | 2 | 2 | 4 | 5 | 1 | 1 |
乙 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(2)补全甲班15名学生测试成绩频数分布直方图:
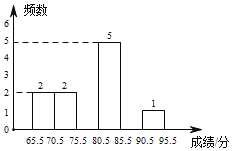
(分析数据)
(3)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 80 | x | 80 | 47.6 |
乙 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(4)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃极分类及投放相关知识合格的学生有 人.
(5)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.