题目内容
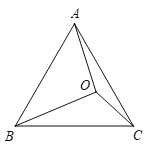
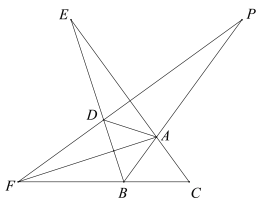
【题目】如图,在等腰△ABC中,AB=AC,![]() ,将点C关于直线AB对称得到点D,作射线BD与CA的延长线交于点E,在CB的延长线上取点F,使得BF=DE,连接AF.
,将点C关于直线AB对称得到点D,作射线BD与CA的延长线交于点E,在CB的延长线上取点F,使得BF=DE,连接AF.

备用图
(1)依题意补全图形;
(2)求证:AF=AE;
(3)作BA的延长线与FD的延长线交于点P,写出一个∠ACB的值,使得AP=AF成立,并证明.
【答案】(1)见解析;(2)证明见解析;(3)∠ACB=54°.证明见解析.
【解析】
根据题意叙述画出图形即可.
(2)由对称可得,DB=BC,∠ABD=∠ABC,再由等量加等量仍是等量可得
BE=CF,易证△ABE ≌ △ACF(SAS),所以 AE=AF.
(3) ∠ACB=54°.由对称和(2)中已证的全等三角形推理可得.
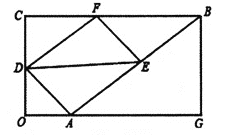
(1)如图所示
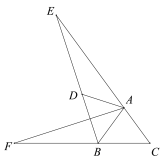
2)证明:∵ 点C与点D关于直线AB对称,
∴ DB=BC,∠ABD=∠ABC.
∵ DE=BF,
∴ DE+BD=BF+BC.
∴ BE=CF.
∵ AB=AC,
∴ ∠ABC=∠C.
∴ ∠ABD=∠C.
∴ △ABE ≌ △ACF(SAS).
∴ AE=AF.
(3)∠ACB=54°.
证明:如图,
∵ AB=AC,
∴ ∠ABC=∠ACB=54°.
∴ ∠BAC=180°-∠ABC-∠C=72°.
∵ 点C与点D关于直线AB对称,
∴ ∠DAB=∠BAC=72°,∠ADB=∠C=54°,AD=AB=AC.
∴ ∠DAE=180°-∠DAB-∠BAC=36°,
∴ ∠E=∠ADB-∠DAE=18°.
∵ 由(2)得,△ABF ≌ △ADE(或者△ACF ≌ △ABE),
∴ ∠AFB=∠E=18°.
∴ ∠BAF=∠ABC-∠AFB=36°=![]() ∠BAD.
∠BAD.
∵ AB=AD,
∴ AF垂直平分BD.
∴ FB=FD.
∴ ∠AFD=∠AFB=18°,
∴ ∠P=∠BAF-∠AFD=18°=∠AFD,
∴ AP=AF.
∵ 由(2)得AE=AF,
∴ AP=AE.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】如图,等边△ABC的边长为3cm,点N在AC边上,AN=1cm.△ABC边上的动点M从点A出发,沿A→B→C运动,到达点C时停止.设点M运动的路程为xcm,MN的长为ycm.
小西根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小西的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
y/cm | 1 | 0.87 | 1 | 1.32 | 2.18 | 2.65 | 2.29 | 1.8 | 1.73 | 1.8 | 2 |
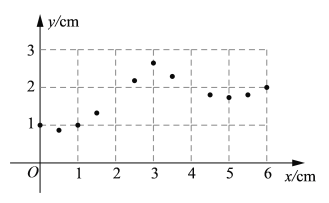
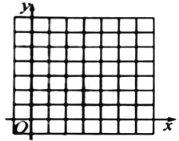
(2)在平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
(3) 结合函数图象,解决问题:当MN=2cm时,点M运动的路程为 cm.
【题目】某商品的进价为每件20元,售价为每件30元,每月可卖出180件,如果该商品计划涨价销售,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)分析数量关系填表:
每台售价(元) | 30 | 31 | 32 | …… | 30+x |
月销售量(件) | 180 | 170 | 160 | …… | _____ |
(2)求y与x之间的函数解析式和x的取值范围
(3)当售价x(元/件)定为多少时,商场每月销售这种商品所获得的利润y(元)最大?最大利润是多少?