题目内容
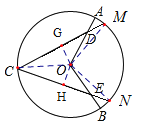
【题目】如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.
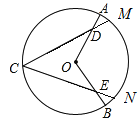
(1)求证:CD=CE.
(2)求证:![]() =
=![]() .
.
【答案】见解析
【解析】
(1)连结CO,证△COD≌△COE,根据全等三角形的性质即可得到CD=CE.
(2)分别连结OM,ON,证∠AOM=∠BON,根据圆心角,弧的关系即可证明.
(1)连结CO,
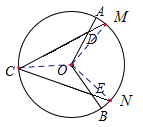
∵在⊙O中,点C是优弧ACB的中点,
∴∠AOC=∠BOC,
∵AD=BE,OA=OB,
∴OD=OE,
在△COD和△COE中,
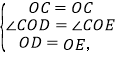
∴△COD≌△COE(SAS),
∴CD=CE.
(2)分别连结OM,ON,过点O作![]()
易证△COG≌△COH(SAS),
得到![]()
根据垂径定理得到![]()
CD=CE.
![]()
![]() △COD≌△COE.
△COD≌△COE.
![]()
![]()
又OD=OE,
![]() △DOM≌△EON(SAS),
△DOM≌△EON(SAS),
∠AOM=∠BON,
![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目