题目内容
如图,已知点C在⊙O上,延长直径AB到点P,连接PC,∠COB=2∠PCB.
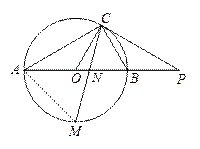
(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧的中点,求MA的长.

(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧的中点,求MA的长.
(1)∵OA=OC,
∴∠OAC=∠OCA.
∴∠COB=2∠OCA.
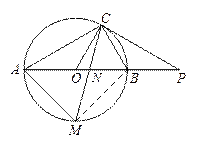 ∵
∵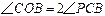
∴∠OCA=∠PCB.………………………1分
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠OCA+∠OCB=90°.
∴∠PCB +∠OCB=90°.
∴∠PCO=90°, ………………………2分
∵点C在⊙O上,
∴PC是⊙O的切线. ………………………3分
(2) 连结BM.
∵M是⊙O下半圆弧中点
∴ 弧AM=弧BM,
∴AM=BM.
∵AB是⊙O直径,
∴∠AMB=90°.
∴∠BAM=∠ABM =45°
∵AC=PC,
∴∠OAC=∠P=∠OCA=∠PCB.
∵OC=OB,
∴∠OBC=∠OCB=2∠PCB.
∵∠PCO=90°,
∴∠PCB=∠P=∠OAC=∠OCA=30°.
∠OBC=∠OCB="60" °.
∵PB=3,
∴BC=3,
∴AB="6." ……………………………4分
在Rt△ABM中,∠AMB =90°,
根据勾股定理,得AM=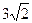 . ……………………………5分
. ……………………………5分
∴∠OAC=∠OCA.
∴∠COB=2∠OCA.
 ∵
∵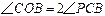
∴∠OCA=∠PCB.………………………1分
∵AB是⊙O直径,
∴∠ACB=90°,

∴∠OCA+∠OCB=90°.
∴∠PCB +∠OCB=90°.
∴∠PCO=90°, ………………………2分
∵点C在⊙O上,
∴PC是⊙O的切线. ………………………3分
(2) 连结BM.
∵M是⊙O下半圆弧中点
∴ 弧AM=弧BM,
∴AM=BM.
∵AB是⊙O直径,
∴∠AMB=90°.
∴∠BAM=∠ABM =45°
∵AC=PC,
∴∠OAC=∠P=∠OCA=∠PCB.
∵OC=OB,
∴∠OBC=∠OCB=2∠PCB.
∵∠PCO=90°,
∴∠PCB=∠P=∠OAC=∠OCA=30°.
∠OBC=∠OCB="60" °.
∵PB=3,
∴BC=3,
∴AB="6." ……………………………4分
在Rt△ABM中,∠AMB =90°,
根据勾股定理,得AM=
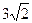 . ……………………………5分
. ……………………………5分略

练习册系列答案
相关题目
 ⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为
⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为 秒.
秒.

 ,
, 为⊙O的弦,点
为⊙O的弦,点 在
在 ,
, ,
, ,则
,则 的长为 .
的长为 .
 是
是 上的两个点,
上的两个点, 是直径,若
是直径,若 ,则
,则 等于( )
等于( )
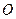 ,
, 点坐标为
点坐标为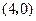 ,
,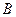 点坐标为
点坐标为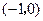 ,以
,以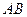 的中点
的中点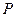 为圆心,
为圆心,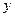 轴的正半轴交于点
轴的正半轴交于点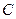 .
.
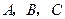 三点的抛物线对应的函数表达式.
三点的抛物线对应的函数表达式.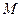 为(1)中抛物线的顶点,求直线
为(1)中抛物线的顶点,求直线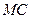 对应的函数表达式.
对应的函数表达式.