题目内容
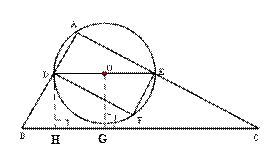
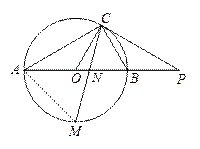
(6分)如图,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A以每秒1个单位长度的速度向点B运动(点D不与B重合),过点D作DE∥BC交AC于点E.以DE为直径作 ⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为
⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为 秒.
秒.

(1)用含 的代数式表示△DEF的面积S;
的代数式表示△DEF的面积S;
(2)当 为何值时,⊙O与直线BC相切?
为何值时,⊙O与直线BC相切?
 ⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为
⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为 秒.
秒.
(1)用含
 的代数式表示△DEF的面积S;
的代数式表示△DEF的面积S;(2)当
 为何值时,⊙O与直线BC相切?
为何值时,⊙O与直线BC相切?解:(1)∵DE∥BC,∴∠ADE=∠B=60°
在△ADE中,∵∠A=90°
∴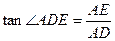
∵AD=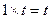 ,∴AE=
,∴AE=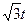 ……………………2分
……………………2分
又∵四边形ADFE是矩形,
∴S△DEF=S△ADE= (
(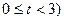
∴S=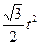 (
(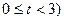 ………………3分
………………3分
(2)过点O作OG⊥BC于G,过点D作DH⊥BC于H,
∵DE∥BC,∴OG=DH,∠DHB=90°
在△DBH中,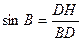
 ∵∠B=60°,BD=
∵∠B=60°,BD=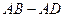 ,AD=
,AD= ,AB=3,
,AB=3,
∴DH=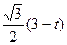 ,∴OG=
,∴OG=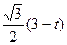 ……………………4分
……………………4分
当OG=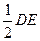 时,⊙O与BC相切,
时,⊙O与BC相切,
在△ADE中,∵∠A=90°,∠ADE=60°,∴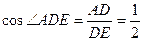 ,
,
∵AD= ,∴DE=2AD=
,∴DE=2AD=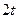 ,
,
∴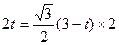 ,
,
∴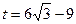
∴当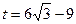 时,⊙O与直线BC相切……………………6分
时,⊙O与直线BC相切……………………6分

在△ADE中,∵∠A=90°
∴
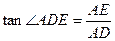
∵AD=
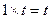 ,∴AE=
,∴AE=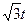 ……………………2分
……………………2分又∵四边形ADFE是矩形,
∴S△DEF=S△ADE=
 (
(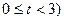
∴S=
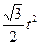 (
(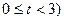 ………………3分
………………3分(2)过点O作OG⊥BC于G,过点D作DH⊥BC于H,
∵DE∥BC,∴OG=DH,∠DHB=90°
在△DBH中,
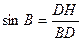
 ∵∠B=60°,BD=
∵∠B=60°,BD=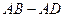 ,AD=
,AD= ,AB=3,
,AB=3,∴DH=
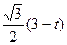 ,∴OG=
,∴OG=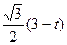 ……………………4分
……………………4分当OG=
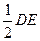 时,⊙O与BC相切,
时,⊙O与BC相切,在△ADE中,∵∠A=90°,∠ADE=60°,∴
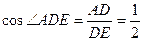 ,
,∵AD=
 ,∴DE=2AD=
,∴DE=2AD=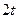 ,
,∴
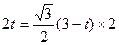 ,
,∴
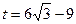
∴当
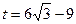 时,⊙O与直线BC相切……………………6分
时,⊙O与直线BC相切……………………6分略

练习册系列答案
相关题目
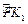 ,
,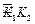 ,
,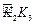 ,
,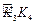 ,
,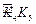 ,
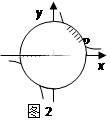
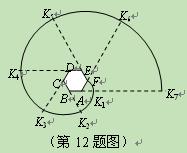
,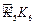 ,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )
,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )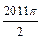
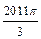
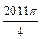
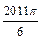
 的周长为
的周长为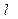 ,面积为S,内切圆
,面积为S,内切圆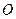 的半径为
的半径为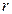 ,探究
,探究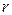 与S、
与S、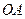 ,
,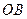 ,
,

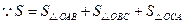
 ,
,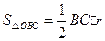 ,
,

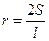
 :
:
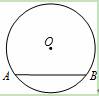
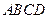 存在内切圆(与各边都相切的圆),如图23—2且面积为
存在内切圆(与各边都相切的圆),如图23—2且面积为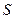 ,各边长分别为
,各边长分别为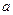 ,
,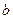 ,
,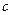 ,
, ,试推导四边形的内切圆半径公式;
,试推导四边形的内切圆半径公式;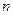 边形(
边形( ,
,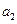 ,
, ,
, ,
, ,合理猜想其内切圆半径公式(不需说明理由).
,合理猜想其内切圆半径公式(不需说明理由).