题目内容
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
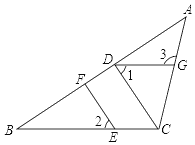
(1)试说明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度数.
【答案】(1)DG∥BC,详见解析;(2)∠3 =103°.
【解析】
(1)先根据垂直定义得出∠CDF=∠EFB=90°,根据平行线判定可得出CD∥EF,故可得出∠2=∠BCD,推出∠1=∠BCD,根据平行线的判定即可得出结论;
(2)先根据CD⊥AB得出∠BDC=90°,由直角三角形的性质得出∠BCD的度数,故可得出∠ACB的度数,再根据平行线的性质即可得出结论.
解:(1)DG∥BC.
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF.
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC;
(2)∵CD⊥AB,
∴∠BDC=90°.
∵∠B=34°,
∴∠BCD=90°-34°=56°.
∵∠ACD=47°,
∴∠ACB=∠ACD+∠BCD=47°+56°=103°.
∵由(1)知DG∥BC,
∴∠3=∠ACB=103°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目