ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘Ύ“ΜΧθΒά¬Ζ…œΘ§ΦΉ¥”AΒΊ≥ωΖΔΒΫBΒΊΘ§““¥”BΒΊ≥ωΖΔΒΫAΒΊΘ§““ΒΡΥΌΕ» «80«ßΟΉ/–Γ ±Θ§ΝΫ»ΥΆ§ ±≥ωΖΔΗςΉ‘ΒΫ¥ο÷’ΒψΚσΆΘ÷ΙΘ§…η–– ΜΙΐ≥Χ÷–ΦΉΓΔ““÷°ΦδΒΡΨύάκΈΣs«ßΟΉΘ§ΦΉ–– ΜΒΡ ±ΦδΈΣt–Γ ±Θ§s”κt÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–ΥΒΖ®¥μΈσΒΡ «Θ®ΓΓΓΓΘ©
A.““≥ωΖΔ1–Γ ±”κΦΉ‘ΎΆΨ÷–œύ”ω
B.ΦΉ¥”AΒΊΒΫ¥οBΒΊ–η–– Μ3–Γ ±
C.ΦΉ‘Ύ1.5–Γ ±ΚσΖ≈¬ΐΥΌΕ»–– Μ
D.““ΒΫ¥οAΒΊ ±ΦΉάκBΒΊΜΙ”–60Η…ΟΉ
ΓΨ¥πΑΗΓΩC
ΓΨΫβΈωΓΩ
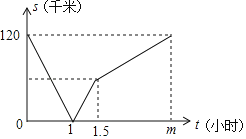
±ΨΧβ÷–ΗυΨίΆΦœώΩ…÷Σ1–Γ ± «ΝΫ»Υœύ”ωΘ§1.5–Γ ± ±Τδ÷–“Μ»ΥΒΫ¥ο÷’ΒψΆΘ÷Ι‘ΥΕ·Θ§m–Γ ± ±ΝΫ’ΏΕΦΆΘ÷Ι‘ΥΕ·Θ§Ω…¥”ΆΦ÷–’“ΒΫΝΫΒΊœύΨύ120«ßΟΉΘ§”÷”…““ΒΡΥΌΕ» «80«ßΟΉ/–Γ ±Ω…ΦΤΥψ≥ωΦΉΒΡΥΌΕ»Θ§‘ΌΗυΨίΦΉΒΡΥΌΕ»«σ≥ωΦΉΒΫ¥ο““ΒΊΥυ”Ο ±ΦδΘ°
ΫβΘΚ”…ΆΦΩ…÷ΣΘ§
““≥ωΖΔ1–Γ ±”κΦΉ‘ΎΆΨ÷–œύ”ωΘ§Ι ―ΓœνA’ΐ»ΖΘΜ
ΦΉΒΡΥΌΕ»ΈΣΘΚ120Γ¬1©¹80ΘΫ40«ßΟΉ/–Γ ±Θ§
‘ρΦΉ¥”AΒΊΒΫ¥οBΒΊ–η–– Μ120Γ¬40ΘΫ3Θ®–Γ ±Θ©Θ§Ι ―ΓœνB’ΐ»ΖΘΜ
Β±““¥οΒΫAΒΊ ±Θ§ΦΉάκBΒΊΒΡΨύάκ «ΘΚ120©¹120Γ¬80ΓΝ40ΘΫ60Θ®«ßΟΉΘ©Θ§Ι ―ΓœνD’ΐ»ΖΘΜ
”…”ΎmΒΡ÷Β≤Μ÷ΣΘ§Ι ΦΉ‘Ύ1.5–Γ ±ΚσΥΌΕ» «ΖώΗΡ±δ≤ΜΡή»ΖΕ®Θ§Ι ―ΓœνC¥μΈσΘΜ
Ι ―ΓΘΚCΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ»γΆΦΘ§¬©Κχ «“Μ÷÷Ι≈¥ζΦΤ ±ΤςΘ°‘ΎΥϋΡΎ≤Ω Δ“ΜΕ®ΝΩΒΡΥ°Θ§Υ°¥”Κχœ¬ΒΡ–ΓΩΉ¬©≥ωΘ°ΚχΡΎ±Ύ”–ΩΧΕ»Θ§»ΥΟ«ΗυΨίΚχ÷–Υ°ΟφΒΡΈΜ÷ΟΦΤΥψ ±ΦδΘ°”ΟxΘ®–Γ ±Θ©±μ Ψ¬©Υ° ±ΦδΘ§yΘ®άεΟΉΘ©±μ ΨΚχΒΉΒΫΥ°ΟφΒΡΗΏΕ»Θ§Ρ≥¥ΈΦΤ ±Ιΐ≥Χ÷–Θ§Φ«¬ΦΒΫ≤ΩΖ÷ ΐΨί»γœ¬±μΘΚ
¬©Υ° ±ΦδxΘ®–Γ ±Θ© | Γ≠ | 3 | 4 | 5 | 6 | Γ≠ |
ΚχΒΉΒΫΥ°ΟφΗΏΕ»yΘ®άεΟΉΘ© | Γ≠ | 9 | 7 | 5 | 3 | Γ≠ |
Θ®1Θ©Έ y”κxΒΡΚ· ΐΙΊœΒ τ”Ύ“Μ¥ΈΚ· ΐΓΔΕΰ¥ΈΚ· ΐΚΆΖ¥±»άΐΚ· ΐ÷–ΒΡΡΡ“Μ÷÷ΘΩ«σ≥ωΗΟΚ· ΐΫβΈω ΫΦΑΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©«σΗ’ΩΣ ΦΦΤ ± ±ΚχΒΉΒΫΥ°ΟφΒΡΗΏΕ»Θ°