Question

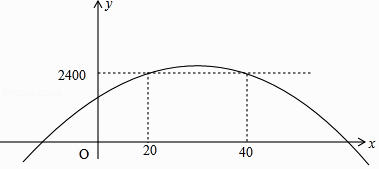
【题目】荆州市某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价p（元/千克）与时间第t（天）之间的函数关系为： ，日销售量y（千克）与时间第t（天）之间的函数关系如图所示：

（1）求日销售量y与时间t的函数关系式？
（2）哪一天的日销售利润最大？最大利润是多少？
（3）该养殖户有多少天日销售利润不低于2400元？
（4）在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠m（m＜7）元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围．

Answer 1

【答案】
（1）解：设解析式为y=kt+b，

将（1，198）、（80，40）代入，得：

，解得： ，

∴y=﹣2t+200（1≤x≤80，t为整数）

（2）解：设日销售利润为w，则w=（p﹣6）y，

①当1≤t≤40时，w=（ t+16﹣6）（﹣2t+200）=﹣ （t﹣30）2+2450，

∴当t=30时，w最大=2450；

②当41≤t≤80时，w=（﹣ t+46﹣6）（﹣2t+200）=（t﹣90）2﹣100，

∴当t=41时，w最大=2301，

∵2450＞2301，

∴第30天的日销售利润最大，最大利润为2450元

（3）解：由（2）得：当1≤t≤40时，

w=﹣ （t﹣30）2+2450，

令w=2400，即﹣ （t﹣30）2+2450=2400，

解得：t1=20、t2=40，

由函数w=﹣ （t﹣30）2+2450图象可知，当20≤t≤40时，日销售利润不低于2400元，

而当41≤t≤80时，w最大=2301＜2400，

∴t的取值范围是20≤t≤40，

∴共有21天符合条件

（4）解：设日销售利润为w，根据题意，得：

w=（ t+16﹣6﹣m）（﹣2t+200）=﹣ t2+（30+2m）t+2000﹣200m，

其函数图象的对称轴为t=2m+30，

∵w随t的增大而增大，且1≤t≤40，

∴由二次函数的图象及其性质可知2m+30≥40，

解得：m≥5，

又m＜7，

∴5≤m＜7

【解析】（1）根据函数图象，利用待定系数法求解可得；（2）设日销售利润为w，分1≤t≤40和41≤t≤80两种情况，根据“总利润=每千克利润×销售量”列出函数解析式，由二次函数的性质分别求得最值即可判断；（3）求出w=2400时x的值，结合函数图象即可得出答案；（4）依据（2）中相等关系列出函数解析式，确定其对称轴，由1≤t≤40且销售利润随时间t的增大而增大，结合二次函数的性质可得答案．