题目内容
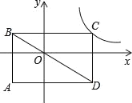
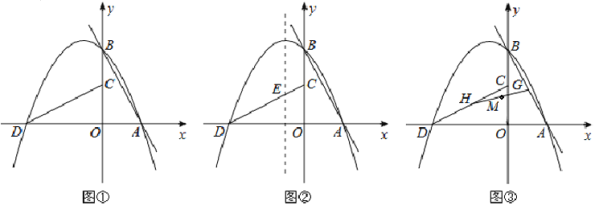
【题目】如图①,定义:直线![]() (m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(1) 若![]() ,则纠缠抛物线P的函数解析式是 .
,则纠缠抛物线P的函数解析式是 .
(2) 判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
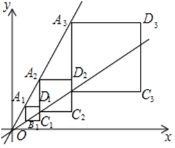
(3) 如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
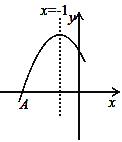
(4) 如图③,在(3)的条件下,G为线段AB上的一个动点,G点随着△AOB旋转到线段CD上的H点,连接H、G,取HG的中点M,当点G从A开始运动到B点,直接写出点M的运动路径长。
【答案】解:(1)![]() ;(2)详见解析;(3)Q点坐标为
;(2)详见解析;(3)Q点坐标为![]() 或
或![]() ;(4)M的运动路径长为
;(4)M的运动路径长为![]()
【解析】
(1)根据题意及直线l解析式可得A,B,D坐标,用待定系数法可求抛物线P的函数解析式;
(2)分别在x=0时和y=0时,求两函数与坐标轴交点,然后根据“互为纠缠线”的定义进行判断;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标;
(4)如图,过点H,G分别作HJ⊥x轴,GK⊥x轴,由旋转的性质可证明△HJO≌△OKG,则可以设点G(m,-2m+4)(0≤m≤2), H(2m-4,m),得到M点坐标为(![]() ),从而确定出点M在直线
),从而确定出点M在直线![]() (-2≤x≤1)上运动,然后根据两点间距离公式易得结果.
(-2≤x≤1)上运动,然后根据两点间距离公式易得结果.
解:(1)若![]() ,则A(1,0),B(0,2),D(-2,0),
,则A(1,0),B(0,2),D(-2,0),
设抛物线解析式为:y=a(x-1)(x+2),
将B(0,2)代入可得:a=-1,
∴抛物线解析式为:y=-(x-1)(x+2)=![]() ;
;
(2)当x=0时,![]() ,
,![]() ,
,
∴两函数图像交于y轴(0,2k),
当y=0时,①![]() ,解得:x=k,
,解得:x=k,
②![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴两函数图像交于x轴(k,0),且OB=OD,
∴![]() 与
与![]() “互为纠缠线”;
“互为纠缠线”;
(3)若![]() ,则A(2,0),B(0,4),C(0,2),D(-4,0),
,则A(2,0),B(0,4),C(0,2),D(-4,0),
求得直线CD的解析式为:y=![]() ,
,
可求得P的对称轴为![]() .
.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y=![]() ,
,
∵点E、点C的横坐标相差1,
∴点F、点Q的横坐标也是相差1.
则|xF(1)|=|xF+1|=1,
解得xF=0或xF=2.
∵点F在直线l:y=2x+4上,
∴点F坐标为(0,4)或(2,8).
若F(0,4),则直线FQ为:y=![]() +4,
+4,
当x=1时,y=![]() ,
,
∴Q1(1,![]() );
);
若F(2,8),则直线FQ为:y=![]() x+9,
x+9,
当x=1时,y=![]() ,
,
∴Q2(1,![]() ).
).
∴满足条件的点Q有2个,点Q坐标为Q1(1,![]() ), Q2(1,
), Q2(1,![]() ).
).
(4)如图,过点H,G分别作HJ⊥x轴,GK⊥x轴,
∵OH=OG,∠HOG=90°,
∴∠HOJ+∠GOK=90°,
∵∠HOJ+∠JHO=90°,
∴∠GOK=∠JHO,
又∵∠HJO=∠OKG=90°,
∴△HJO≌△OKG,
设点G(m,-2m+4)(0≤m≤2),则H(2m-4,m)
∴M(![]() ),
),
令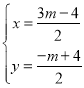 ,
,
∴ ,
,
∴![]() ,
,
∵0≤m≤2,
∴-2≤x≤1,
∴点M在直线![]() (-2≤x≤1)上运动,
(-2≤x≤1)上运动,
当x=1时,y=![]() ,
,
当x=-2时,y=![]() ,
,
∴M的运动路径长=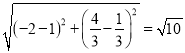


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案