题目内容
【题目】如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.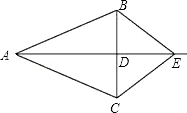
(1)求证:△ABE≌△ACE;
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
【答案】
(1)证明:∵AB=AC,点D为BC的中点,
∴∠BAE=∠CAE,
∵AE=AE
∴△ABE≌△ACE(SAS)
(2)解:当AE=2AD(或AD=DE或DE= ![]() AE)时,四边形ABEC是菱形
AE)时,四边形ABEC是菱形
理由如下:
∵AE=2AD,∴AD=DE,
又∵点D为BC中点,
∴BD=CD,
∴四边形ABEC为平行四边形,
∵AB=AC,
∴四边形ABEC为菱形
【解析】(1)用SAS可证△ABE≌△ACE;(2)先由有两组对边分别相等的四边形是平行四边形可证四边形ABEC为平行四边形,再由有一组邻边相等的平行四边形是菱形可证四边形ABEC为菱形。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目