题目内容
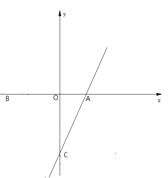
【题目】如图,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,交
,交![]() 轴于点
轴于点![]() ,连接直线
,连接直线![]() .
.
(1)求二次函数的解析式;
(2)点![]() 在二次函数的图像上,圆
在二次函数的图像上,圆![]() 与直线
与直线![]() 相切,切点为
相切,切点为![]() .
.
①若![]() 在
在![]() 轴的左侧,且△
轴的左侧,且△![]() ∽△
∽△![]() ,求点
,求点![]() 的坐标;
的坐标;
②若圆![]() 的半径为4,求点
的半径为4,求点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为y=x2 +x-2;(2)①点P的坐标为(﹣1,﹣2)或(![]() ,
, ![]() );②点P的坐标为(
);②点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)将A、B两点的坐标代入抛物线的解析式,得到关于a、b的二元一次方程组,从而可求得a、b的值;
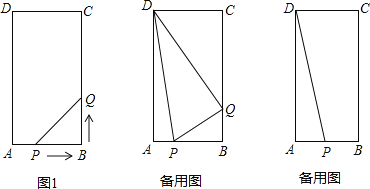
(2)①由切线的性质可知PH⊥AC,当H在点C下方时,由△CHP∽△AOC可知∠PCH=∠CAO从而可证明CP∥x轴,于是得到yP=-2,yP=-2代入抛物线的解析式可求得x1=0(舍去),x2=-1,从而可求得P(-1,-2);如图1,当H′在点C上方时,由相似三角形的性质可知:∠P′CH′=∠CAO,故此QA=QC,设OQ=m,则QC=QA=m+1,在Rt△QOC中,由勾股定理可求得m的值,从而得到点Q的坐标,然后利用待定系数法求得直线CP′的解析式为y=-![]() x-2,然后将CP′与抛物线的解析式联立可求得点P′的坐标为(-
x-2,然后将CP′与抛物线的解析式联立可求得点P′的坐标为(-![]() ,
, ![]() ).
).
(3)在x轴上取一点D,如图(2),过点D作DE⊥AC于点E,使DE=4.在Rt△AOC中,由勾股定理可知AC=![]() ,由题意可知证明△AED∽△AOC,由相似三角形的性质可求得AD=2
,由题意可知证明△AED∽△AOC,由相似三角形的性质可求得AD=2![]() ,故此可得到点D的坐标为D(1-2
,故此可得到点D的坐标为D(1-2![]() ,0)或D(1+2
,0)或D(1+2![]() ,0),过点D作DP∥AC,交抛物线于P,利用待定系数法可求得直线AC的解析式为y=2x-2,于是得到直线PD的解析式为y=2x+4
,0),过点D作DP∥AC,交抛物线于P,利用待定系数法可求得直线AC的解析式为y=2x-2,于是得到直线PD的解析式为y=2x+4![]() -2或y=2x-4
-2或y=2x-4![]() -2,将直线PD的解析式与抛物线的解析式联立可求得点P的坐标.
-2,将直线PD的解析式与抛物线的解析式联立可求得点P的坐标.
试题解析:(1)∵将x=1,y=0,x=-2,y=0代入y=ax2+bx-2得![]() ,解得:
,解得: ![]()
∴抛物线的解析式为y=x2+x-2.
(2)解①∵圆P与直线AC相切,
∴PH⊥span>AC.
(i)如图1,当H在点C下方时,
①∵△CHP∽△AOC,
∴∠PCH=∠CAO.
∴CP∥x轴.
∴yP=-2.
∴x2+x-2=-2.
解得x1=0(舍去),x2=-1,
∴P(-1,-2).
(ii)如图1,当H′在点C上方时.
∵∠P′CH′=∠CAO,
∴QA=QC,
设OQ=m,则QC=QA=m+1,
在Rt△QOC中,由勾股定理,得m2+22=(m+1)2,解得,m=![]() ,即OQ=
,即OQ=![]() ;
;
设直线CP′的解析式为y=kx-2,
把Q(-![]() ,0)的坐标代入,得
,0)的坐标代入,得![]() k-2=0,解得k=-
k-2=0,解得k=-![]() ,∴y=-
,∴y=-![]() x-2,
x-2,
由-![]() x-2=x2+x-2,解得x1=0(舍去),x2=
x-2=x2+x-2,解得x1=0(舍去),x2=![]() ,此时y=-
,此时y=-![]() ×(-
×(-![]() )-2=
)-2=![]() ,
,
∴P′(-![]() ,
, ![]() ).
).
∴点P的坐标为(-1,-2)或(-![]() ,
, ![]() )
)
②在x轴上取一点D,如图(2),过点D作DE⊥AC于点E,使DE=4.
在Rt△AOC中,AC=![]() ,
,
∵∠COA=∠DEA=90°,∠OAC=∠EAD,
∴△AED∽△AOC.
∴![]() ,即
,即![]() ,解得AD=2
,解得AD=2![]() ,
,
∴D(1-2![]() ,0)或D(1+2
,0)或D(1+2![]() ,0).
,0).
过点D作DP∥AC,交抛物线于P,设直线AC的解析式为y=kx+b.
将点A、C的坐标代入抛物线的解析式得到: ![]()
解得: ![]()
∴直线AC的解析式为y=2x-2.
∴直线PD的解析式为y=2x+4![]() -2或y=2x-4
-2或y=2x-4![]() -2,
-2,
当2x+4![]() -2=x2+x-2时,即x2-x-4
-2=x2+x-2时,即x2-x-4![]() =0,解得x1=
=0,解得x1=![]() ,x2=
,x2=![]() ;
;
当2x-4![]() -2=x2+x-2时,即x2-x+4
-2=x2+x-2时,即x2-x+4![]() =0,方程无实数根.
=0,方程无实数根.
∴点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,-
,-![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
这些数据说明:植物每天高度增长量![]() 关于温度
关于温度![]() 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.