题目内容
在平面直角坐标系xOy中,二次函数y=-x2+(m-1)x+4m的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
(1)求m的值及点A的坐标;
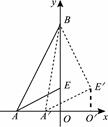
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.

(1)求m的值及点A的坐标;
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.
(1)m="1,A(-2,0);" (2)①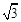 ,②点E′的坐标是(1,1),③点E′的坐标是(
,②点E′的坐标是(1,1),③点E′的坐标是(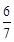 ,1).
,1).
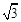 ,②点E′的坐标是(1,1),③点E′的坐标是(
,②点E′的坐标是(1,1),③点E′的坐标是(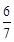 ,1).
,1).试题分析:(1)将点代入解析式即可求出m的值,这样写出函数解析式,求出A点坐标;
(2)①将E点的坐标代入二次函数解析式,即可求出AA′;②连接EE′,构造直角三角形,利用勾股定理即可求出A′B2+BE′2 当n=1时,其最小时,即可求出E′的坐标;③过点A作AB′⊥x轴,并使AB′ =" BE" = 3.易证△AB′A′≌△EBE′,当点B,A′,B′在同一条直线上时,A′B + B′A′最小,即此时A′B+BE′取得最小值.易证△AB′A′∽△OBA′,由相似就可求出E′的坐标
试题解析:
解:(1)由题意可知4m=4,m=1.
∴二次函数的解析式为
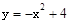 .
.∴点A的坐标为(-2,0).
(2)①∵点E(0,1),由题意可知,
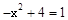 .
.解得
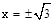 .
.∴AA′=
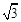 .
.②如图,连接EE′.
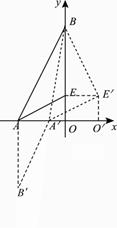
由题设知AA′=n(0<n<2),则A′O=2-n.
在Rt△A′BO中,由A′B2=A′O2+BO2,
得A′B2=(2–n)2+42=n2-4n+20.
∵△A′E′O′是△AEO沿x轴向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=n.
又BE=OB-OE=3.
∴在Rt△BE′E中,BE′2=E′E2+BE2=n2+9,
∴A′B2+BE′2=2n2-4n+29=2(n–1)2+27.
当n=1时,A′B2+BE′2可以取得最小值,此时点E′的坐标是(1,1).
③如图,过点A作AB′⊥x轴,并使AB′=BE=3.
易证△AB′A′≌△EBE′,
∴B′A′=BE′,
∴A′B+BE′=A′B+B′A′.
当点B,A′,B′在同一条直线上时,A′B+B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
∴
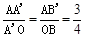 ,
,∴AA′=
 ,
,∴EE′=AA′=
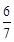 ,
,∴点E′的坐标是(
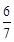 ,1).
,1).
练习册系列答案
相关题目
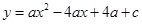 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
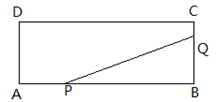

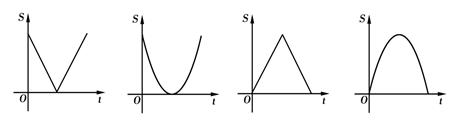
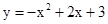 取最大值时,x= .
取最大值时,x= .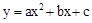 中,其函数
中,其函数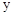 与自变量
与自变量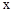 之间的部分对应值如下表所示:
之间的部分对应值如下表所示: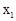 ,
,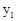 )、B(
)、B( ,
,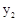 )在函数的图象上,则当
)在函数的图象上,则当
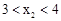 时,
时,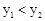 B.
B. C.
C.