题目内容
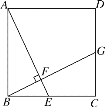
【题目】如图,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.
(1)求证:△ABF∽△BGC;
(2)若AB=2,G是CD的中点,求AF的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据正方形的性质得出∠ABE=∠BCG=90°,进而得出∠BAE=∠CBG,再利用相似三角形的判定证明即可;
(2)根据(1)中的相似三角形,利用其性质解答即可.
(1)∵在正方形ABCD中,
∴∠ABE=∠BCG=90°,
∵∠BAE+∠ABF=90°,∠CBG+∠ABF=90°,
∴∠BAE=∠CBG,
∴△ABF∽△CBG;
(2)∵△ABF∽△CBG,
∴![]() ,
,
∵AB=2,G是CD的中点,正方形ABCD,
∴BC=2,CG=1,
∴BG=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:AF=![]() =
=![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】某校举办的八年级学生数学素养大赛共设![]() 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图 | 趣题巧解 | 数学应用 | |
小米 |
|
|
|
小麦 |
|
|
|
![]() 若七巧板拼图,趣题巧解,数学应用三项得分分别
若七巧板拼图,趣题巧解,数学应用三项得分分别![]() 按折算计入总分,最终谁能获胜?
按折算计入总分,最终谁能获胜?
![]() 若七巧板拼图按
若七巧板拼图按![]() 折算,小麦 (填“可能”或“不可能”)获胜.
折算,小麦 (填“可能”或“不可能”)获胜.