题目内容
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.
求证:BF=AC.
【答案】证明:∵CD⊥AB,
∴∠BDC=∠CDA=90°;
∵∠ABC=45°,
∴∠DCB=∠ABC=45°(三角形的内角和定理),
∴DB=DC(等角对等边);
∵BE⊥AC,
∴∠AEB=90°,
∴∠A+∠ABE=90°(直角三角形的两个锐角互为余角);
∵∠CDA=90°,
∴∠A+∠ACD=90°,
∴∠ABE=∠ACD(同角的余角相等);
在△BDF和△CDA中,
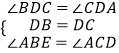 ,
,
∴△BDF≌△CDA(ASA),
∴BF=AC(全等三角形的对应边相等).
【解析】要证BF=AC,就需要证明△BDF和△CDA全等,由已知条件可知它们是直角三角形。抓住题中关键的已知条件∠ABC=45°,CD⊥AB于D,可得到△BDC是等腰直角三角形,得出DB=DC。再根据同角的余角相等或等角的余角相等,可得到两三角形的另一组对应角相等,即可证得结论。
【考点精析】认真审题,首先需要了解余角和补角的特征(互余、互补是指两个角的数量关系,与两个角的位置无关).

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目