Question

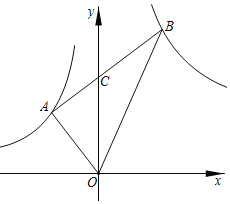
【题目】如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为_____．

Answer 1

【答案】10．

【解析】

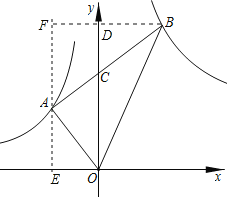
分别过A、B作AE⊥x轴于E，BD⊥y轴交AE于F．设A（a，b），则ab=-4．根据两角对应相等的两三角形相似，得出△OAE∽△ABF，由相似三角形的对应边成比例，则BD、OD都可用含a、b的代数式表示，从而求出B的坐标，进而得出结果．

解：分别过A、B作AE⊥x轴于E，BD⊥y轴交AE于F．设A（a，b）．

∵顶点A在反比例函数y＝图象上，

∴ab＝﹣4．

∵∠OAB＝90°，

∠OAE＝90°﹣∠BAF＝∠ABF，∠OEA＝∠BFA＝90°，

∴△OAE∽△ABF，

∴，

在Rt△AOB中，∠AOAB＝90°，∠OBA＝30°，

∴，

∴，

∴AF＝﹣，BF＝b，

∵Rt△AOB的面积恰好被y轴平分，

∴AC＝BC，

∴BD＝DF＝BF＝﹣a，OD＝AE+AF＝b﹣a，

∴b＝﹣a，

∴A（﹣b，b），B（b，b﹣）

∴﹣bb＝﹣4，

∴b2＝，

∴k＝b（b﹣）＝b2﹣ab＝10，

故答案为：10．