Question

【题目】（1）在直角坐标系中画出二次函数y＝x2﹣x﹣的图象．

（2）若将y＝x2﹣x﹣图象沿x轴向左平移2个单位，请写出平移后图象所对应的函数关系式．

（3）根据图象，写出当y＞0时，x的取值范围．

Answer 1

【答案】（1）见解析；（2）y＝x2+x﹣ ；（3）x＜﹣1或x＞3

【解析】

（1）先将抛物线化为顶点式后，根据抛物线的顶点坐标、对称轴，与坐标轴的交点坐标即可画出图象．
（2）先将抛物线化为顶点式后，由于沿x轴向左平移2个单位，从而列出函数式．
（3）根据图像即可求出y＞0时，x的取值范围．

解：（1）∵y＝x2﹣x﹣=（x-1）2-2，

∴抛物线的顶点坐标（1，-2），对称轴x=1，

∵y＝0时，x2﹣x﹣=0，解得：x=3或x=-1，

即抛物线与x轴的交点坐标为（-1，0）和（3，0），

当x=0时，y= -，
即抛物线与y轴交点坐标为（0，-），

∴二次函数y＝x2﹣x﹣的图象如图：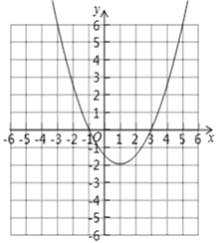

（2）∵y＝x2﹣x﹣=（x-1）2-2
∴将y＝x2﹣x﹣图象沿x轴向左平移2个单位，
则y=（x-1+2）2-2=x2+x﹣，

∴平移后图象所对应的函数关系式为：y＝x2+x﹣；

（3）根据图象得，当y＞0时，x＜-1或x＞3．