Question

【题目】如图有一圆锥形粮堆，其主视图是边长为6m的正三形ABC。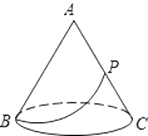

（1）求该圆锥形粮堆的侧面积。
（2）母线AC的中点P处有一老鼠正在偷吃粮食，小猫从B处沿圆锥表面去偷袭老鼠，求小猫经过的最短路程。(结果不取近似数)

Answer 1

【答案】
（1）解：∵主视图是边长为6m的正三形ABC，
∴AB母线AB=R=6m，
∴底面圆的半径r=3m，
∴S侧=rR=×3×6=18（m2），

（2）解：∵△ABC为正三角形，
∴BC=6，
∴l=2π×3=6π，

根据底面圆的周长等于展开后扇形的弧长，得： =6π，

故n=180°，则∠BAC=90°，

∴BP= =3 m

答：小猫所经过的最短路程是3 m.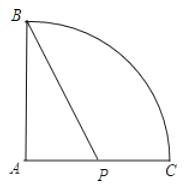

【解析】（1）由圆锥的侧面展开图是扇形，再根据圆锥的侧面积公式=×r×R计算即可.
（2）根据两点之间，线段最短；依题可得展开的是圆锥的半个侧面，再连接BP，再根据勾股定理计算即可.
【考点精析】利用弧长计算公式和扇形面积计算公式对题目进行判断即可得到答案，需要熟知若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．