题目内容
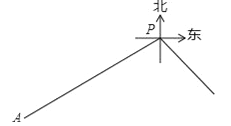
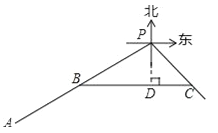
【题目】如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口PC=2x,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(结果精确到个位,参考数据:![]() ,
,![]() ,
, ![]() )
)
【答案】每小时20海里.
【解析】
试题分析:根据题意构造直角三角形,求出BP,在Rt△BPD中求出PD,然后在Rt△PDC中表示出PD,继而建立方程可解出x的值.
试题解析:设乙船速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,PC=2x,过P作PD⊥BC于D,则BP=86﹣2×15=56(海里),在Rt△PDB中,∠PDB=90°,∠BPD=60°,∴PD=PBcos60°=28(海里),在Rt△PDC中,∠PDC=90°,∠DPC=45°,∴PD=PCcos45°=![]() ,∴
,∴![]() ,即
,即![]() ≈20(海里).
≈20(海里).
答:乙船的航行速度为每小时20海里.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目