题目内容
【题目】如图，已知像这样由7个全等的正六边形组成的图形叫做“二环蜂窝”，每个正六边形的顶点叫做格点，顶点都在格点上的三角形叫做格点三角形．已知△ABC为该二环蜂窝一个格点三角形，则在该二环蜂窝中，以点A为顶点且与△ABC相似（包括全等但不与△ABC重合）的格点三角形最多能作的个数为（ ）
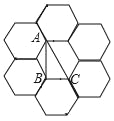
A. 18 B. 23 C. 25 D. 28
【答案】D
【解析】
先说明三角形ABC是30度的直角三角形，分两类找符合条件的三角形：①相似比为1的，根据一个正六边形，以斜边不同找三角形的个数为6，三个正六边形为：3×6﹣1=17个；②找相似比不为1的，以斜边不同，同理可得结论．
∵7个全等的正六边形，
∴△ABC三个内角分别为30°，60°，90°，
①如图1，
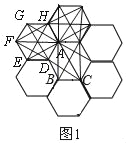
与△ABC全等时，在正六边形ADEFGH中，以AF为斜边的有4个：△AFG，△AFH，△AFE，△AFD，以DG为斜边的有△ADG，以EH为斜边的有△AEH，同理另外以点A为顶点的两个正六边形各有6个全等的三角形，去掉△ABC本身，所以一共有17个三角形；
②如图2，
与△ABC相似的，以AA'为斜边的有4个，以AD为斜边的有4个，以C'B'为斜边的有△AB'C'，以BB'为斜边的有△ABB'，以D'H为斜边的有△AHD'，所以一共有11个，
综上所述，以点A为顶点且与△ABC相似（包括全等但不与△ABC重合）的格点三角形最多能作的个数为：17+11=28（个）；
故选：D．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
【题目】为了对某市区全民阅读状况进行调查和评估，有关部门随机抽取了部分市民进行每天阅读时间情况的调查，并根据调查结果制做了如下尚不完整的频数分布表（被调查者每天的阅读时间均在0﹣120分钟之内）
阅读时间x（分钟） | 0≤x＜30 | 30≤x＜60 | 60≤x＜90 | 90≤x≤120 |
频数 | 450 | 400 | m | 50 |
频率 | 0.45 | 0.4 | 0.1 | n |
（1）被调查的市民人数为多少，表格中，m，n为多少；
（2）补全频数分布直方图；
（3）某市区目前的常住人口约有118万人，请估计该市区每天阅读时间在60～120分钟的市民大约有多少万人？
