Question

如图（5），A、B、C是二次函数y=ax2＋bx＋c（a≠0）的图像上三点,根据图中给出的三点的位置,可得a_______0，c________0, ⊿________0.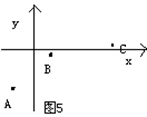

Answer 1

<、<、>

解析分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解：画草图得，此函数开口向下，所以a＜0；
与与y轴的交点为在y轴的负半轴上，所以c＜0；
抛物线与x轴有两个交点，∴b²-4ac＞0．
故a＜0，c＜0，△＞0．
点评：考查二次函数y=ax²+bx+c系数符号的确定．