题目内容
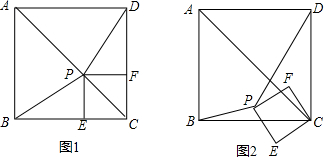
如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.(1)试说明:BP=DP;
(2)如图2,若正方形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请画图用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与正方形PECF的两个顶点连接,使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论;
(4)旋转的过程中AP和DF的长度是否相等,若不等,直接写出AP:DF=
(5)若正方形ABCD的边长是4,正方形PECF的边长是1.把正方形PECF绕点C按逆时针方向旋转的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
分析:(1)利用三角形全等证明PB=PD.
(2)通过反例说明,如点P在正方形的边上.
(3)由旋转的特点找到DF和BE,再利用三角形全等证明它们相等.
(4)通过特殊位置如图1可判断它们是否相等,也可求出它们的比.
(5)把面积的最值问题转化为三角形的高即C点到BD距离大小问题.
(2)通过反例说明,如点P在正方形的边上.
(3)由旋转的特点找到DF和BE,再利用三角形全等证明它们相等.
(4)通过特殊位置如图1可判断它们是否相等,也可求出它们的比.
(5)把面积的最值问题转化为三角形的高即C点到BD距离大小问题.
解答: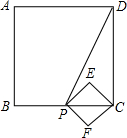 解:(1)∵AC是正方形ABCD的对角线,
解:(1)∵AC是正方形ABCD的对角线,
∴∠BAP=∠DAP=45°,BA=DA,又AP为公共边,
∴△BAP≌△DAP,
∴PB=PD;
(2)不是总有BP=DP.如图,当P点在BC上时,显然DP>BP,
(3)BE=DF.
证明如下:如图2,连DF,BE.
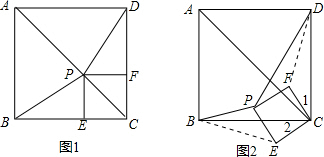
∵∠1+∠FCB=∠2+∠FCB=90°,
∴∠1=∠2,
又∵CF=CE,CD=CB,
∴△CDF≌△CBE,(SAS)
∴BE=DF;
(4)旋转的过程中AP和DF的长度不相等.它们的比值不变,AP:DF=
:1.
理由如下:如图
过B点作BM⊥BE,且BM=BE.则△BMA≌△CEM.所以∠AMB=∠BEC,EC=AM.由(3)得BM=BE=DF,
又∵EC=PE,
∴AM=PE,而∠3=∠AMB-135°,∠4=∠BEC-90°-45°,
∴∠3=∠4,
∴四边形AMEP是平行四边形,
∴AP=ME,
由(3)得BM=BE=DF,
所以AP=
BE=
DF.
故填
:1.
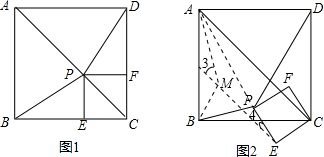
(5)正方形PECF绕点C按逆时针方向旋转的过程中,△PBD的面积存在最大值和最小值,
当P点到BD的距离最小时,△PBD的面积最小,而P点到C点的距离不变,
所以CP⊥BD时,△PBD的面积最小,此时P点在AC上,
S△BDP=
×4
×
=4,
当P点到BD的距离最大时,△PBD的面积最大,而P点到C点的距离不变.
所以CP⊥BD时,△PBD的面积最大,此时P点在AC的延长线上.S△BDP=
×4
×3
=12.
 解:(1)∵AC是正方形ABCD的对角线,
解:(1)∵AC是正方形ABCD的对角线,∴∠BAP=∠DAP=45°,BA=DA,又AP为公共边,
∴△BAP≌△DAP,
∴PB=PD;
(2)不是总有BP=DP.如图,当P点在BC上时,显然DP>BP,
(3)BE=DF.
证明如下:如图2,连DF,BE.

∵∠1+∠FCB=∠2+∠FCB=90°,
∴∠1=∠2,
又∵CF=CE,CD=CB,
∴△CDF≌△CBE,(SAS)
∴BE=DF;
(4)旋转的过程中AP和DF的长度不相等.它们的比值不变,AP:DF=
| 2 |
理由如下:如图
过B点作BM⊥BE,且BM=BE.则△BMA≌△CEM.所以∠AMB=∠BEC,EC=AM.由(3)得BM=BE=DF,
又∵EC=PE,
∴AM=PE,而∠3=∠AMB-135°,∠4=∠BEC-90°-45°,
∴∠3=∠4,
∴四边形AMEP是平行四边形,
∴AP=ME,
由(3)得BM=BE=DF,
所以AP=
| 2 |
| 2 |
故填
| 2 |

(5)正方形PECF绕点C按逆时针方向旋转的过程中,△PBD的面积存在最大值和最小值,
当P点到BD的距离最小时,△PBD的面积最小,而P点到C点的距离不变,
所以CP⊥BD时,△PBD的面积最小,此时P点在AC上,
S△BDP=
| 1 |
| 2 |
| 2 |
| 2 |
当P点到BD的距离最大时,△PBD的面积最大,而P点到C点的距离不变.
所以CP⊥BD时,△PBD的面积最大,此时P点在AC的延长线上.S△BDP=
| 1 |
| 2 |
| 2 |
| 2 |
点评:熟悉正方形的性质和三角形全等的判定定理,熟练掌握旋转的性质.

练习册系列答案
相关题目
 ,求出t值;若不能,说明理由.(同学可在图2中画草图)
,求出t值;若不能,说明理由.(同学可在图2中画草图)