��Ŀ����
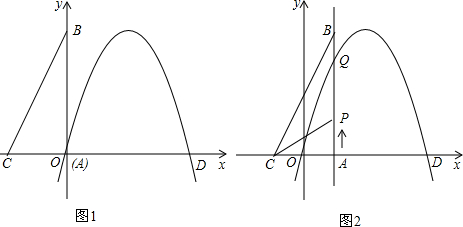
��ͼl����֪�����߾�������ԭ��O��x������һ��D�����������Ϊ��2��4����ֱ��������ABC�Ķ���A���O�غϣ�AC��AB�ֱ���x�ᣬy���ϣ���AC=3��AB=4��
��1��ֱ��BC�Ľ���ʽΪ
��2����������ߵĺ�����ϵʽ��
��3����ֱ��������ABC��ÿ��1����λ���ȵ��ٶȴ�ͼ1��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��2����AB����������ߵĽ���ΪQ����ͼ2��ʾ����
�����CPQ�����ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��ֱ��д��ֱ��BC����������Ψһ�Ĺ�����ʱt��ֵ��
��1��ֱ��BC�Ľ���ʽΪ
y=
x+4
| 4 |
| 3 |
y=
x+4
��| 4 |
| 3 |
��2����������ߵĺ�����ϵʽ��
��3����ֱ��������ABC��ÿ��1����λ���ȵ��ٶȴ�ͼ1��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��2����AB����������ߵĽ���ΪQ����ͼ2��ʾ����
�����CPQ�����ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��ֱ��д��ֱ��BC����������Ψһ�Ĺ�����ʱt��ֵ��

��������1���������B��C�����꣬����ֱ��BC�Ľ���ʽ��
��2�����ݶ���ʽֱ����������߽���ʽ���ɣ�
��3���ٸ�������ó�P��Q�����꣬�����ó�PQ�ij������ɵó���CPQ��������������䷽���ó���ֵ��
�ڸ��ݵ�ֱ��BC����������Ψһ�Ĺ�����ʱ�����ʱֱ�߽���ʽΪ��y=
x+d���ó�
x+d=-x2+4x��������x2-
x+d=0��ʱ������������ȵ�ʵ������
�����ó�d��ֵ�����ɵó�ͼ����x�ύ�����꣬���ɵó��ƶ����룮
��2�����ݶ���ʽֱ����������߽���ʽ���ɣ�
��3���ٸ�������ó�P��Q�����꣬�����ó�PQ�ij������ɵó���CPQ��������������䷽���ó���ֵ��
�ڸ��ݵ�ֱ��BC����������Ψһ�Ĺ�����ʱ�����ʱֱ�߽���ʽΪ��y=
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
�����ó�d��ֵ�����ɵó�ͼ����x�ύ�����꣬���ɵó��ƶ����룮
����⣺��1����ֱ��������ABC�Ķ���A���O�غϣ�AC��AB�ֱ���x�ᣬy���ϣ���AC=3��AB=4��
��C��B����ֱ�Ϊ��C��-3��0����B��0��4����
��BCֱ�߽���ʽΪ��y=ax+b��
��
��ã�
��
��y=
x+4��
�ʴ�Ϊ��y=
x+4��
��2���������ߵĶ�������Ϊ��2��4����
���������߽���ʽΪ��y=a��x-2��2+4��
�������߹�ԭ�㣬
��0=4a+4��
��ã�a=-1��
��������ߵĽ���ʽΪ��y=-��x-2��2+4����y=-x2+4x��
��3����������ó���P������Ϊ����t��t������Q������Ϊ����t��-t2+4t����
��PQ=-t2+4t-t=-t2+3t��
���CPQ�����Ϊ
S=
PQ•AC
=
��3����-t2+3t��
=-
��t2-3t��
=-
��t-
��2+
��S�������ֵ�����ֵ��
��
�ڵ�ֱ��BC����������Ψһ�Ĺ�����ʱ��
���ʱֱ�߽���ʽΪ��y=
x+d��
��
x+d=-x2+4x��������x2-
x+d=0��ʱ������������ȵ�ʵ������
��b2-4ac=
-4��1��d=0��
��ã�d=
��
���ʱBC����ֱ�߽���ʽΪ��y=
x+
��
��y=0ʱ��x=-
��
��C��ӣ�-3��0������-
��0���ƶ���
����λ���ȣ�
��ֱ��BC����������Ψһ�Ĺ�����ʱt��ֵΪ��
��
��C��B����ֱ�Ϊ��C��-3��0����B��0��4����
��BCֱ�߽���ʽΪ��y=ax+b��
|
��ã�
|
��y=
| 4 |
| 3 |
�ʴ�Ϊ��y=
| 4 |
| 3 |
��2���������ߵĶ�������Ϊ��2��4����
���������߽���ʽΪ��y=a��x-2��2+4��
�������߹�ԭ�㣬
��0=4a+4��
��ã�a=-1��
��������ߵĽ���ʽΪ��y=-��x-2��2+4����y=-x2+4x��
��3����������ó���P������Ϊ����t��t������Q������Ϊ����t��-t2+4t����
��PQ=-t2+4t-t=-t2+3t��
���CPQ�����Ϊ
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
��S�������ֵ�����ֵ��
| 27 |
| 8 |
�ڵ�ֱ��BC����������Ψһ�Ĺ�����ʱ��
���ʱֱ�߽���ʽΪ��y=
| 4 |
| 3 |
��
| 4 |
| 3 |
| 8 |
| 3 |
��b2-4ac=
| 64 |
| 9 |
��ã�d=
| 16 |
| 9 |
���ʱBC����ֱ�߽���ʽΪ��y=
| 4 |
| 3 |
| 16 |
| 9 |
��y=0ʱ��x=-
| 4 |
| 3 |
��C��ӣ�-3��0������-
| 4 |
| 3 |
| 5 |
| 3 |
��ֱ��BC����������Ψһ�Ĺ�����ʱt��ֵΪ��
| 5 |
| 3 |
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ��䷽������ֵ�Լ������б�ʽ�ʹ���ϵ������һ�κ�������ʽ��֪ʶ���������ν�ϵó���Ӧ��λ���ǽ���ؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��֪1�¡�7�¡�9�º�12�����ĸ��µ���ƽ���۸�ֱ�Ϊ8Ԫ/ǧ�ˡ�26Ԫ/ǧ�ˡ�14Ԫ/ǧ�ˡ�11Ԫ/ǧ�ˣ�
��֪1�¡�7�¡�9�º�12�����ĸ��µ���ƽ���۸�ֱ�Ϊ8Ԫ/ǧ�ˡ�26Ԫ/ǧ�ˡ�14Ԫ/ǧ�ˡ�11Ԫ/ǧ�ˣ� ̽�յơ��������ߡ������Ƶȶ������������ߵ�һ��ԭ���������Ľ��㴦�����Ĺ��߱�����ᱻƽ���������ͼ���ɽ���O�������Ĺ���OB��OC�����������POQƽ�еķ����������֪��ABO=42�㣬��DCO=53�㣬���BOC=
̽�յơ��������ߡ������Ƶȶ������������ߵ�һ��ԭ���������Ľ��㴦�����Ĺ��߱�����ᱻƽ���������ͼ���ɽ���O�������Ĺ���OB��OC�����������POQƽ�еķ����������֪��ABO=42�㣬��DCO=53�㣬���BOC= ��֪1�¡�7�¡�9�º�12�����ĸ��µ���ƽ���۸�ֱ�Ϊ8Ԫ/ǧ�ˡ�26Ԫ/ǧ�ˡ�14Ԫ/ǧ�ˡ�11Ԫ/ǧ�ˣ�
��֪1�¡�7�¡�9�º�12�����ĸ��µ���ƽ���۸�ֱ�Ϊ8Ԫ/ǧ�ˡ�26Ԫ/ǧ�ˡ�14Ԫ/ǧ�ˡ�11Ԫ/ǧ�ˣ� �У�A��BΪx�������㣬C��DΪy���ϵ����㣬��
�У�A��BΪx�������㣬C��DΪy���ϵ����㣬�� ������M��������C2��
������M��������C2�� ��
�� ��0���Ķ��㣮
��0���Ķ��㣮
