Question

如图1，已知直线y=2x（即直线l₁）和直线y=-

1

2

x+4（即直线l₂），l₂与x轴相交于点A．点P从原点O出发，向x轴的正方向作匀速运动，速度为每秒1个单位，同时点Q从A点出发，向x轴的负方向作匀速运动，速度为每秒2个单位．设运动了t秒．
（1）求这时点P、Q的坐标（用t表示）．
（2）过点P、Q分别作x轴的垂线，与l₁、l₂分别相交于点O₁、O₂（如图1）．以O₁为圆心、O₁P为半径的圆与以O₂为圆心、O₂Q为半径的圆能否相切？若能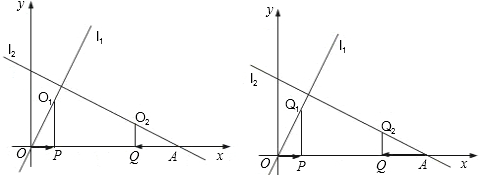，求出t值；若不能，说明理由．（同学可在图2中画草图）

Answer 1

分析：（1）由函数图象和直接得出1点P的横坐标为t，P点的坐标为（t，0），由-

1

2

x+4=0得x=8，所以点Q的横坐标为8-2t，点Q的坐标为（8-2t，0）．
（2）将P，Q的横坐标分别代入其关系式，可求出点O₁，O₂的坐标，分别求出两圆外切与内切时t满足的条件，求出t的值，舍去不符合条件的．

解答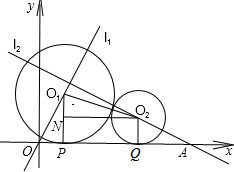：解：（1）点P的横坐标为t，P点的坐标为（t，0），
由-

1

2

x+4=0得x=8，
所以点Q的横坐标为8-2t，点Q的坐标为（8-2t，0）．（3分）

（2）由（1）可知点O₁的横坐标为t，点O₂的横坐标为8-2t，
将x=t代入y=2x，得y=2t，
所以点O₁的坐标为（t，2t），
将x=8-2t代入y=-

1

2

x+4，得y=t，
所以点O₂的坐标为（8-2t，t），（5分）
①若这两圆外切（如图），连接O₁O₂，过点O₂作O₂N⊥O₁P，垂足为N．
则O₁O₂=2t+t=3t，O₂N=8-2t-t=8-3t，O₁N=2t-t=t，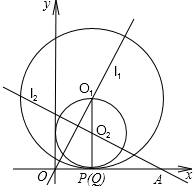
所以t²+（8-3t）²=（3t）²，（7分）
即t²-48t+64=0，解得t₁=24+16

2

，t₂=24-16

2

．（9分）
②若这两圆内切，又因为两圆都x轴相切所以点P、Q重合（如图）
此时O₁、O₂的横坐标相同，即8-2t=t，t=

8

3

，（10分）
（或：设l₂与y轴相交于点M，则

AP

AO

=

O2P

MO

，即

8-t

8

=

t

4

，
所以t=

8

3

，
所以两圆能相切，这是t的值分别为24+16

2

，24-16

2

和

8

3

．

点评：此题很复杂，把动点问题与圆相结合，提高了难度，解答此题的关键是根据题意画出图形，结合图形解答．