题目内容
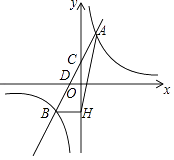
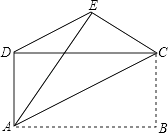
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( ) 
A.①
B.②
C.①②
D.①②③
【答案】D
【解析】解:∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90°,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF(①正确)
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,∠BDF=∠CDE,
∴△BDF≌△CDE(②正确)
∴DF=DE,
连接AD,
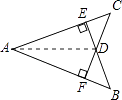
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上(③正确)
故选D.
【考点精析】通过灵活运用角平分线的性质定理,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.

练习册系列答案
相关题目