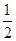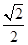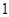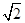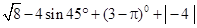题目内容
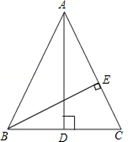
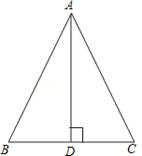
请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
如图,正确画出图形,
(1)∵AB=AC,AD⊥BC,AD=BC,
∴BD= BC=
BC= AD.即AD=2BD.
AD.即AD=2BD.
∴AB=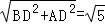 BD.
BD.
∴tanB= ,
,
sinB=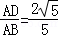 .
.
(2)在Rt△BEC中,sinC=sin∠ABC=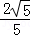 ,
,
又∵sinC=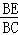 ,
,
∴ .
.
故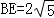 (米).
(米).
(1)∵AB=AC,AD⊥BC,AD=BC,
∴BD=
 BC=
BC= AD.即AD=2BD.
AD.即AD=2BD.∴AB=
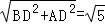 BD.
BD.∴tanB=
 ,
,sinB=
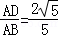 .
.(2)在Rt△BEC中,sinC=sin∠ABC=
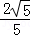 ,
,又∵sinC=
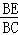 ,
,∴
 .
.故
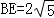 (米).
(米).

(1)本题可根据三角形的特殊性(等腰三角形)和AD=BC,先求出AD和BD,CD的关系,进而求出tan B和sinB的值;
(2)由于是等腰三角形,∠B=∠C,求出了sinB也就是求出了sinC,直角三角形BCE中,已知了BC的长,BE就不难求出了.
(2)由于是等腰三角形,∠B=∠C,求出了sinB也就是求出了sinC,直角三角形BCE中,已知了BC的长,BE就不难求出了.

练习册系列答案
相关题目
 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.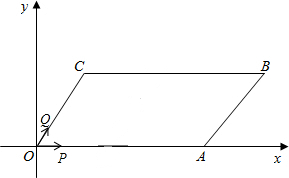
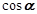 的值是( )
的值是( )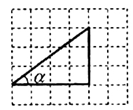
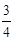
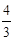
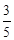
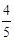
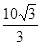 米
米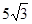 米
米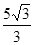 米
米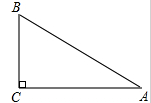
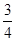
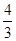
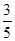
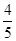
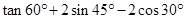 的结果是( )
的结果是( )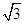
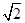
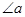 是等腰直角三角形的一个锐角,则
是等腰直角三角形的一个锐角,则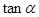 的值是( )
的值是( )