题目内容
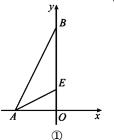
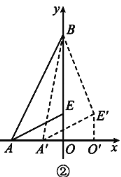
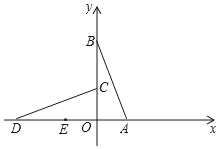
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.
(1)若F为CD上一动点,求出当△DEF与△COD相似时点F的坐标;
(2)过E作x轴的垂线l,在直线l上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点的坐标;若不存在,请说明理由.
【答案】(1)F(﹣1,![]() )或F(﹣
)或F(﹣![]() ,
,![]() );(2)Q(﹣1,2)或(﹣1,﹣1).
);(2)Q(﹣1,2)或(﹣1,﹣1).
【解析】
(1)当△DEF∽△COD时,![]() ,DF=DEcos∠CDO=
,DF=DEcos∠CDO=![]() ,据此求出EF的长度和点F的坐标即可;
,据此求出EF的长度和点F的坐标即可;
(2)首先以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′,由圆周角定理,可得∠CQO=∠CQ′O=∠CDO,在Rt△CDO中,由勾股定理可得CD=![]() ,则PQ=
,则PQ=![]() CD=
CD=![]() ;然后求出点P的坐标是多少;设Q(﹣1,a),则(
;然后求出点P的坐标是多少;设Q(﹣1,a),则(![]() )2+(a﹣
)2+(a﹣![]() )2=
)2=![]() ,据此求出a的值是多少,进而求出Q点坐标是多少即可.
,据此求出a的值是多少,进而求出Q点坐标是多少即可.
(1)∵A(1,0),B(0,3),
∴OA=1,OB=3,
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴OC=1,OD=3,
∴C(0,1),D(﹣3,0),
如图1,当△DEF∽△COD时,![]() ,
,
∴EF=![]() ,
,
∴F(﹣1,![]() );
);
当△DEF∽△COD时,DF=DEcos∠CDO=![]() ,
,
作FK⊥OD于K,
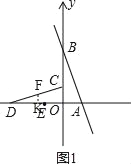
则FK=DFsin∠CDO=![]() ,DK=DFcos∠CDO=
,DK=DFcos∠CDO=![]() ,
,
∴F(﹣![]() ,
,![]() );
);
(2)如图2,以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′,

由圆周角定理,
可得∠CQO=∠CQ′O=∠CDO,
在Rt△CDO中,由勾股定理可得CD=![]() ,
,
则PQ=![]() CD=
CD=![]() ,
,
又∵P为CD中点,P(﹣![]() ,
,![]() ),
),
设Q(﹣1,a),
则(![]() )2+(a﹣
)2+(a﹣![]() )2=
)2=![]() ,
,
解得a=2或﹣1,
∴Q(﹣1,2)或(﹣1,﹣1).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目