题目内容
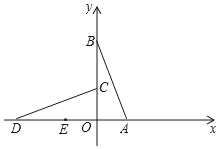
【题目】在平面直角坐标系中,已知点A(-2,0),点B(0,4),点E在OB上,且∠OAE=∠OBA.
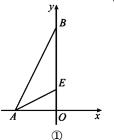
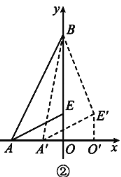
(1)如图①,求点E的坐标
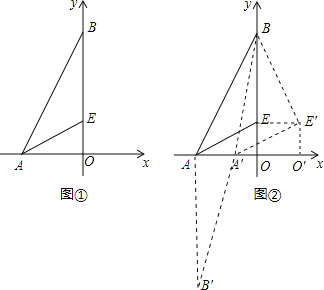
(2)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.
①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).
【答案】(1)(0,1)(2)①(1,1);②(![]() ,1).
,1).
【解析】
(1)根据相似三角形△OAE∽△OBA的对应边成比例得到![]() ,则易求OE=1,所以E(0,1);
,则易求OE=1,所以E(0,1);
(2)如图②,连接EE′.在Rt△A′BO中,勾股定理得到A′B2=(2-m)2+42=m2-4m+20,在Rt△BE′E中,利用勾股定理得到BE′2=E′E2+BE2=m2+9,则A′B2+BE′2=2m2-4m+29=2(m-1)2+27.所以由二次函数最值的求法知,当m=1即点E′的坐标是(1,1)时,A′B2+BE′2取得最小值.
(1)如图①,∵点A(-2,0),点B(0,4),
∴OA=2,OB=4.
∵∠OAE=∠0BA,∠EOA=∠AOB=90°,
∴△OAE∽△OBA,
∴![]() ,即
,即![]() ,
,
解得OE=1,
∴点E的坐标为(0,1);
(2)①如图②,连接EE′.
由题设知AA′=m(0<m<2),则A′O=2-m.
在Rt△A′BO中,由A′B2=A′O2+BO2,得A′B2=(2-m)2+42=m2-4m+20.
∵△A′E′O′是△AEO沿x轴向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=m.
又∵BE=OB-OE=3,
∴在Rt△BE′E中,BE′2=E′E2+BE2=m2+9,
∴A′B2+BE′2=2m2-4m+29=2(m-1)2+27.
当m=1时,A′B2+BE′2可以取得最小值,此时,点E′的坐标是(1,1).
②如图②,过点A作AB′⊥x,并使AB′=BE=3.
易证△AB′A′≌△EBE′,
∴B′A′=BE′,
∴A′B+BE′=A′B+B′A′.
当点B、A′、B′在同一条直线上时,A′B+B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
∴![]() ,
,
∴![]() ,AO=2,
,AO=2,
∴AA′=![]() ×2=
×2=![]() ,
,
∴EE′=AA′=![]() ,
,
∴点E′的坐标是(![]() ,1).
,1).

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案