题目内容
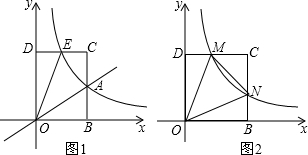
在平面直角坐标系xOy中,矩形OBCD的顶点B在x轴正半轴上,顶点D在y轴正半轴上.
(1)如图1,反比例函数y=
(x>0)的图象与正比例函数y=
x的图象交于点A. BC边经过点A,CD边与反比例函数图象交于点E,四边形OACE的面积为6.
①直接写出点A的坐标;
②判断线段CE与DE的大小关系,并说明理由;
(2)如图2,若反比例函数y=
(x>0)的图象与CD交点M,与BC交于点N,CM=nDM(n>0),连接OM,ON,MN,设M点的横坐标为t(t>0).求:
(用含n的式子表示).
(1)如图1,反比例函数y=
| 6 |
| x |
| 2 |
| 3 |
①直接写出点A的坐标;
②判断线段CE与DE的大小关系,并说明理由;
(2)如图2,若反比例函数y=
| k |
| x |
| S△CMN |
| S△OMN |

考点:反比例函数综合题
专题:探究型
分析:(1)①把反比例函数与正比例函数的解析式组成方程组即可求出A点坐标;
②连接OC,根据反比例函数系数k的几何意义得出△ODE与△OAB的面积,再根据四边形OACE的面积为6求出矩形OBCD的面积,由此即可得出结论;
(2)过点M作ME⊥x轴于点E,由于点M、N是反比例函数y=
图象上的点,故可得出S△OME=S△
OBN,所以S△OMN=S矩形EBNM,设点M(t,
),则C((n+1)t,
),E(t,0),B((n+1)t,0),N((n+1)t,
),再根据三角形的面积公式即可得出结论.
②连接OC,根据反比例函数系数k的几何意义得出△ODE与△OAB的面积,再根据四边形OACE的面积为6求出矩形OBCD的面积,由此即可得出结论;
(2)过点M作ME⊥x轴于点E,由于点M、N是反比例函数y=
| 6 |
| x |
OBN,所以S△OMN=S矩形EBNM,设点M(t,
| k |
| t |
| k |
| t |
| k |
| (n+1)t |
解答: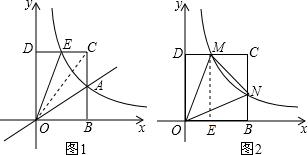 解:(1)①∵点A是反比例函数y=
解:(1)①∵点A是反比例函数y=
(x>0)的图象与正比例函数y=
x的图象的交点,
∴
,
解得
(舍去)或
∴A(3,2);
②如图1,连接OC,
∵点A、E均是反比例函数y=
图象上的点,
∴S△ODE=S△OAB=3,
∵四边形OACE的面积为6,
∴S矩形OBCD=S△ODE+S△OAB+S四边形OACE=3+3+6=12,
∵四边形OBCD是矩形,
∴S△OCD=
S矩形OBCD=
×12=6,
∴S△OED=S△OCE,
∵两三角形的高相等,
∴CE=DE;
(2)如图2,过点M作ME⊥x轴于点E,
∵点M、N是反比例函数y=
图象上的点,
∴S△OME=S△OBN,
∴S△OMN=S矩形EBNM,
设点M(t,
),则C((n+1)t,
),E(t,0),B((n+1)t,0),N((n+1)t,
),
∴S△CMN=
CM•CN=
nt•(
-
)=
nk(1-
);
S△OMN=S矩形EBNM=
(ME+BN)•BE=
(
+
)•nt=
nk(1+
),
∴
=
=
.
 解:(1)①∵点A是反比例函数y=
解:(1)①∵点A是反比例函数y=| 6 |
| x |
| 2 |
| 3 |
∴
|
解得
|
|
∴A(3,2);
②如图1,连接OC,
∵点A、E均是反比例函数y=
| 6 |
| x |
∴S△ODE=S△OAB=3,
∵四边形OACE的面积为6,
∴S矩形OBCD=S△ODE+S△OAB+S四边形OACE=3+3+6=12,
∵四边形OBCD是矩形,
∴S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△OED=S△OCE,
∵两三角形的高相等,
∴CE=DE;
(2)如图2,过点M作ME⊥x轴于点E,
∵点M、N是反比例函数y=
| 6 |
| x |
∴S△OME=S△OBN,
∴S△OMN=S矩形EBNM,
设点M(t,
| k |
| t |
| k |
| t |
| k |
| (n+1)t |
∴S△CMN=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| t |
| k |
| (n+1)t |
| 1 |
| 2 |
| 1 |
| n+1 |
S△OMN=S矩形EBNM=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| t |
| k |
| (n+1)t |
| 1 |
| 2 |
| 1 |
| n+1 |
∴
| S△CMN |
| S△OMN |
| ||||
|
| n |
| n+2 |
点评:本题考查的是反比例函数综合题,涉及到反比例函数系数k的几何意义、矩形的性质、反比例函数与一次函数的交点问题等相关知识,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
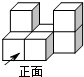 如图是由7个完全相同的小正方体组成的几何体,其俯视图是 ( )
如图是由7个完全相同的小正方体组成的几何体,其俯视图是 ( )A、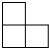 |
B、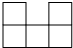 |
C、 |
D、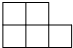 |
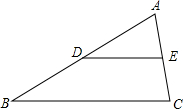 如图,在△ABC中,D、E分别是AB、AC的中点,S△ADE=1,则S四边形BCED=
如图,在△ABC中,D、E分别是AB、AC的中点,S△ADE=1,则S四边形BCED=