题目内容
(1)解方程:x2+4x-2=0;
(2)解不等式组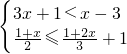 .
.
解:(1)移项,得
x2+4x=2,
在方程两边加上4,得
x2+4x+4=6,
∴(x+2)2=6,
∴x+2=± ,
,
∴x1=-2+ ,x2=-2
,x2=-2
(2)
解不等式①,得
x<-2,
解不等式②,
得x≥-5
∴原不等式组的解集为:
-5≤x<-2.
分析:(1)先移项,把常数项移到等号右边,再根据等式的性质在方程两边同时加上4,将方程得左边配成一个完全平方式,最后用直接开平方法解就可以了.
(2)将不等式组的两个不等式分别表上序号后,再分别求出两个不等式的解集,从而求出不等式组的解集.
点评:本题考查了使用配方法解一元二次方程得运用以及解不等式组的方法得使用,在解答中要求学生掌握解高次方程得基本思想是降次,不等式组的解集的确定办法.
x2+4x=2,
在方程两边加上4,得
x2+4x+4=6,
∴(x+2)2=6,
∴x+2=±
 ,
,∴x1=-2+
 ,x2=-2
,x2=-2
(2)

解不等式①,得
x<-2,
解不等式②,
得x≥-5
∴原不等式组的解集为:
-5≤x<-2.
分析:(1)先移项,把常数项移到等号右边,再根据等式的性质在方程两边同时加上4,将方程得左边配成一个完全平方式,最后用直接开平方法解就可以了.
(2)将不等式组的两个不等式分别表上序号后,再分别求出两个不等式的解集,从而求出不等式组的解集.
点评:本题考查了使用配方法解一元二次方程得运用以及解不等式组的方法得使用,在解答中要求学生掌握解高次方程得基本思想是降次,不等式组的解集的确定办法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目