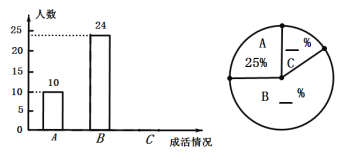
题目内容
【题目】如图,AB是⊙O的直径,AB=20,DA⊥AB,E是⊙O上一点,连接DE并延长交AB的延长线于点F,DE=DA,BF=16.
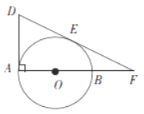
(1)求证:DE是⊙O的切线.
(2)求AD的长
【答案】(1)见解析;(2)DA=15.
【解析】
(1)构造△DAO≌△DEO,即可得证;
(2)利用切线的性质和勾股定理构建方程,即可求出AD.
(1)连接OE,OD,如图所示:
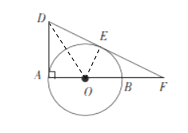
∵OA=OE,OD=OD,DA=DE
∴△DAO≌△DEO(SSS)
∵DA⊥AB
∴∠DAO=∠DEO=90°,即OE⊥DE
∴DE是⊙O的切线;
(2)∵AB=20
∴OE=OB=10
∵BF=16
∴OF=OB+BF=10+16=26
∴![]()
∵DA=DE,AF=AB+BF=20+16=36,DF=DE+EF=AD+24
∴![]()
![]()
∴![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目