题目内容
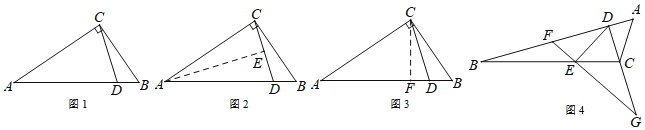
【题目】如图,正方形![]() 边长为2,
边长为2,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上两动点,且满足
上两动点,且满足![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
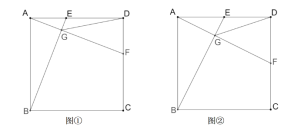
(1)如图1,判断线段![]() 、
、![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)在(1)的条件下,连接![]() ,直接写出
,直接写出![]() 的最小值为 ;
的最小值为 ;
(3)如图2,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
①求证:![]() 平分
平分![]() ;
;
②求线段![]() 的长度.
的长度.
【答案】(1)![]() ;理由见解析;(2)
;理由见解析;(2)![]() ;(3)①见解析;②
;(3)①见解析;②![]() .
.
【解析】
(1)证明![]() ,即可解答.
,即可解答.
(2)取AB的中点0,连接OG、OD,则OG=![]() AB=1,在Rt△AOD中,根据勾股定理计算出OD的值;根据三角形的三边关系,可得OG+DG>OD,于是当O、D、G三点共线时,DG的长度最小为OD-OG,据此解答.
AB=1,在Rt△AOD中,根据勾股定理计算出OD的值;根据三角形的三边关系,可得OG+DG>OD,于是当O、D、G三点共线时,DG的长度最小为OD-OG,据此解答.
(3)①过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,可得四边形
,可得四边形![]() 为矩形,再证得
为矩形,再证得![]() ,所以
,所以![]() ,又因为
,又因为![]() ,
, ![]() ,可得
,可得![]() 平分
平分![]() ;
;
②在![]() 中,根据
中,根据![]() ,可求得DN,在
,可求得DN,在![]() 中,
中,![]() ,
,![]() ,即可求得DG.
,即可求得DG.
(1)![]() ;理由:
;理由:
∵四边形![]() 为正方形.
为正方形.
∴![]() ,
,![]() ,
,
∵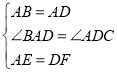 ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)取AB的中点O,连接OG、OD,如图所示:
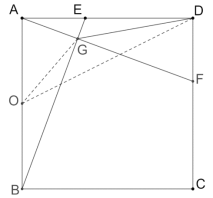
则OG=![]() AB=1
AB=1
在Rt△AOD中,OD=![]()
根据三角形的三边关系,OG+DG>OD,当O、D、G三点共线时,DG的长度最小,最小值=OD-OG=![]()
故答案为:![]()
(3)①过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() .
.
∴四边形![]() 为矩形,
为矩形,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 平分
平分![]() ;
;
②在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.

故答案为:![]()

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目