题目内容
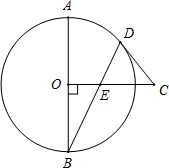
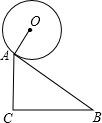
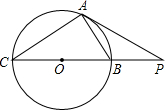
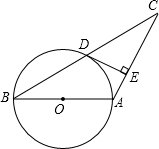
如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
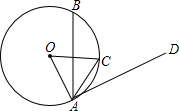
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.

(1)如图,∵AB为⊙O的弦,C为劣弧AB的中点,AB=8,
∴OC⊥AB于E,
∴AE=
AB=4,
又∵AO=5,
∴OE=
=3,
∴CE=OC-OE=2,
在Rt△AEC中,tan∠BAC=
=
=
;
(2)AD与⊙O相切.理由如下:
∵OA=OC,
∴∠C=∠OAC,
∵由(1)知OC⊥AB,
∴∠C+∠BAC=90°.
又∵∠BAC=∠DAC,
∴∠OAC+∠DAC=90°,
∴AD与⊙O相切.

∴OC⊥AB于E,
∴AE=
| 1 |
| 2 |
又∵AO=5,
∴OE=
| OA2-AE2 |
∴CE=OC-OE=2,
在Rt△AEC中,tan∠BAC=
| EC |
| AE |
| 2 |
| 4 |
| 1 |
| 2 |
(2)AD与⊙O相切.理由如下:
∵OA=OC,
∴∠C=∠OAC,
∵由(1)知OC⊥AB,
∴∠C+∠BAC=90°.
又∵∠BAC=∠DAC,
∴∠OAC+∠DAC=90°,
∴AD与⊙O相切.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目