题目内容
关于 的一元二次方程
的一元二次方程 的一个根是2.
的一个根是2.
小题1:求 的值和方程的另一个根
的值和方程的另一个根
小题2:若直线AB经过点A(2,0),B(0, ),求直线AB的解析式;
),求直线AB的解析式;
小题3:在平面直角坐标系中画出直线AB的图象,P是 轴上一动点,是否存在点P,
轴上一动点,是否存在点P,
使△ABP是直角三角形,若存在,求出点P坐标,若不存在,说明理由.
 的一元二次方程
的一元二次方程 的一个根是2.
的一个根是2.小题1:求
 的值和方程的另一个根
的值和方程的另一个根
小题2:若直线AB经过点A(2,0),B(0,
 ),求直线AB的解析式;
),求直线AB的解析式;小题3:在平面直角坐标系中画出直线AB的图象,P是
 轴上一动点,是否存在点P,
轴上一动点,是否存在点P,使△ABP是直角三角形,若存在,求出点P坐标,若不存在,说明理由.

小题1:∵2是一元二次方程
 的一个根,
的一个根,∴
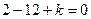 ,
,∴
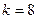 .-----------------------------------------------------------------------------------------2分
.-----------------------------------------------------------------------------------------2分∴一元二次方程为
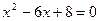 ,
,∴
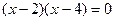 ,
,∴
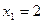 ,
,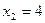
∴一元二次方程为
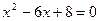 的另一个根
的另一个根 =4.--------------------------------4分
=4.--------------------------------4分小题2:设直线AB的解析式为
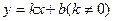
∵直线AB经过点A(2,0),B(0,4)
∴
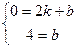
解得
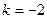 ,
,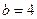 .-------------------------------------------------------------------------------6分
.-------------------------------------------------------------------------------6分直线AB的解析式:
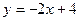 .-------------------------------------------------------------8分
.-------------------------------------------------------------8分小题3:画图正确----------------------------------------------------------------------------------------9分
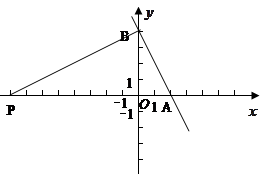
第一种:AB是斜边,∠APB=90°
∵∠AOB=90°,
∴当点P与原点O重合时,∠APB=90°,
∴当点P的坐标为(0,0),△ABP是直角三角形.-----------------------------------------11分
第二种:设AB是直角边,点B为直角顶点,即∠ABP=90°
∵线段AB在第一象限,
∴这时点P在
 轴负半轴.
轴负半轴.设P的坐标为(
 ,0)
,0)∵A(2,0), B(0,4)
∴OA=2,OB=4,OP=
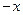 ,
,∴
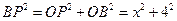 ,
,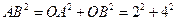 ,
,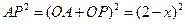 .
.∵
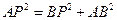 ,
,∴
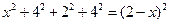 ,
,解得
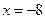
∴当点P的坐标为(―8,0),△ABP是直角三角形.-------------------------------------13分
第三种:设AB是直角边,点A为直角顶点,即∠BAP=90°
∵点A在
 轴上,点P是
轴上,点P是 轴上的动点,
轴上的动点,∴∠BAP>90°
∴∠BAP=90°的情况不存在.-------------------------------------------------------------------14分
∴当点P的坐标为(―8,0)或(0,0)时,△ABP是直角三角形.
略

练习册系列答案
相关题目


 ,
,
 ,
, 

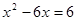
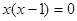 的解是( ).
的解是( ).


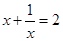 的解为
的解为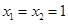 ; (2)
; (2)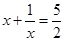 的解为
的解为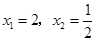 ;
;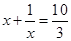 的解为
的解为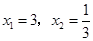 ; …… ……
; …… ……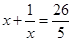 的解为 ;
的解为 ;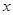 的方程
的方程 的解为
的解为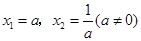 ;
;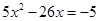 .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程) -4x+3=0,则此三角形的周长是 。
-4x+3=0,则此三角形的周长是 。